2.2 Variationsproblem mit Nebenbedingung

[prev] [prev-tail] [tail] [up]

2.2 Variationsproblem mit Nebenbedingung

Satz 3:

|----------------------------------------------------------------------------------------|
| |
|D sei Teilmenge des Vektorraums Y. Es seien N Nebenbedingungen g1, ..., gN gegeben und F sei auf
|D definiertes Funktional. Es mo¨gen Zahlen c1, ..., cN und ein y (- D derart existieren, daß y [eindeutig
|bestimmte] Minimalfunktion von ~F = F + c1g1 + c2g2 + ...+ cNgN ist. |
|Dann minimiert y das Funktional F [eindeutig] auf der Menge {y (- D|gj(y) = gy(y), j = 1, ..., N}.
-----------------------------------------------------------------------------------------

Mittels g_j(y) = l_j mit l_j = 1, ..., N können die ₁, ..., _N eliminiert werden.

Beweis:

Nach Voraussetzung wissen wir:

F~(y) > ~F(y) A y (- D

Durch Einsetzen von folgt:

sum -- sum N -- F(y)+ cjgj(y) > F(y)+ cjgj(y) A y (- D j=1 j=1

N F (y) > F(y)+ sum cj(gj(y) -gj(y)) A y (- D j=1

Daraus ergibt sich dann:

f(y) > F(y) A y (- D, gj(y) = gj(y) mit j = 1, ..., N

Die nennt man auch Lagrangesche Multiplikatoren.

2.2.1 Oberfläche einer rotierenden Flüssigkeit

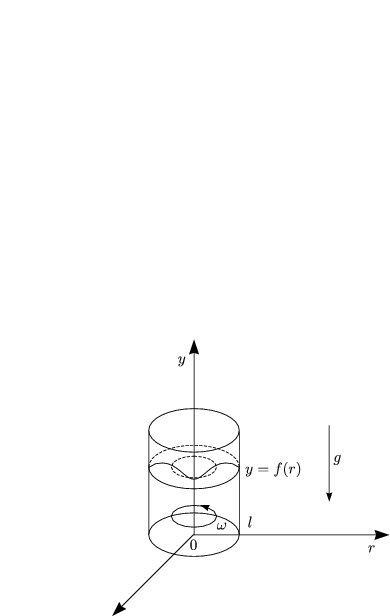
Im Zylinder befindet sich Wasser der konstanten Dichte vom Volumen V . Gesucht ist die sich einstellende freie Oberfläche, die folgendermaßen charakterisiert ist:

Das Volumen V bleibt unverändert.
Die potentielle Energie wird minimal.

Wir berechnet das Volumen der Flüssigkeit:

2 integral p integral l f integral (r) integral l G(y) = V = rdrdfdy = 2p rf(r)dr f=0r=0y=0 r=0

Des weiteren benötigen wir die Energie:

integral [ 1 ] E(f ) = gy dm + 2r2w2dm

Das Massenelement dm kann außerdem aus der Dichte und dem Volumenelement berechnet werden:

dm = r dV

Damit folgt:

integral 2p integral l f integral (r)[ 1 ] integral l[1 1 ] E(f) = gy- - r2w2 rrdrdfdy = 2pr - gf(r)2- -r2w2f(r) r dr = 0r=0y=0 2 r=0 2 2 integral l [ 2 2 2 ] = pr gf(r) - r w f(r) rdr r=0

(2.1)

Formulierung der Aufgabe:

Gesucht ist y = f(r) mit 0 < r < l, die E(f) minimiert auf = {f C[0,l],f(r) > 0} unter der Nebenbedingung g(f) = V . Betrachte nun (f) = E(f) + g(f):

integral l 2 integral l g(f) = 2p rf(r) dr = pr .r . rf (r)dr 0 0

Wir wählen den Multiplikator geschickt:

|--------------------------| integral l | integral l ~ | ~cg(f ) = ~c.2p rf(r)dr =|pr.c . rf(r)dr mit c = 2c| 0 | 0 r | ---------------------------

Dann ist folgendes auf zu untersuchen (Für alle f und alle v [0,l] mit f + v ):

|------------------------------------------| | integral l | E~(f ) = pr [(gf(r)2- r2w2f(r))r + crf(r)]dr | | | ---------r=0--------------------------------

l ~ ~ integral [ 2 3 2 2 3 2 ] E(f + v) - E(f) = pr g(f + b) (r)- r w (f + v)(r)+ cr(f + v)(r)- gf (r)+ rw f(r) -crf (r) dr = r=0 integral l [ ] = pr grv2 + 2grf (r)v(r)- r3w2v(r)+ crv(r) dr r=0

(2.2)

Wir schätzen die Funktion nach unten ab:

l l integral [ 2 ( 2 2 ) ] integral [ 2 2 ] ~E(f+v)- ~E(f) = pr grv + 2gfv- r w v+ cv r dr > pr 2gf- r w + c rv(r)dr r=0 r=0

Das Gleichheitszeichen gilt nur, falls _r=0^lrv² dr = 0, das heißt nur für v(r) = 0 v.

integral l [2gf -r2w2 + c]rv(r) dr = 0 A v mit f + v (- D r=0

Dies bedeutet nach unserer vorherigen Sätzen, daß der Ausdruck in der Klammer gleich Null sein muß:

|----------------------| | 1-( 2 2 ) | |y = f (r) = 2g r w - c | -----------------------

Für y = f(r) = gilt:

~E(f-+ v)- ~E(f) > 0 A v mit f + v (- D und v /= 0

Das wird nun mit V = 2 _r=0^lrf(r)dr eliminiert. f > 0 bedeutet, daß r²² - > 0 und damit < 0. Durch Einsetzen von f für f folgt:

22 22 - c = 2g2V - w-lV - w--l (> 0) pl 2 2

Damit erhalten wir eine Bedingung für :

|----------| | 2 4g | |w < pl4V | -----------

[prev] [prev-tail] [front] [up]