![|----------------------------------------------------------------------------------------|
| |
| integral b |
|E sei g (- C0[a;b] und es gelte g(x)h'(x)dx = 0 A h (- C1[a,b] mit h(a) = h(b) = 0 ( A h (- D0). Dann|
| a |
|ist g(x) = const. A x (- [a,b]. |
-----------------------------------------------------------------------------------------](ma124x.gif)
![|----------------------------------------------------------------------------------------|
| |
| integral b |
|E sei g (- C0[a;b] und es gelte g(x)h'(x)dx = 0 A h (- C1[a,b] mit h(a) = h(b) = 0 ( A h (- D0). Dann|
| a |
|ist g(x) = const. A x (- [a,b]. |
-----------------------------------------------------------------------------------------](ma124x.gif)
Wähle ![]() (x) =
(x) = ![]() ax
ax dt.
dt. 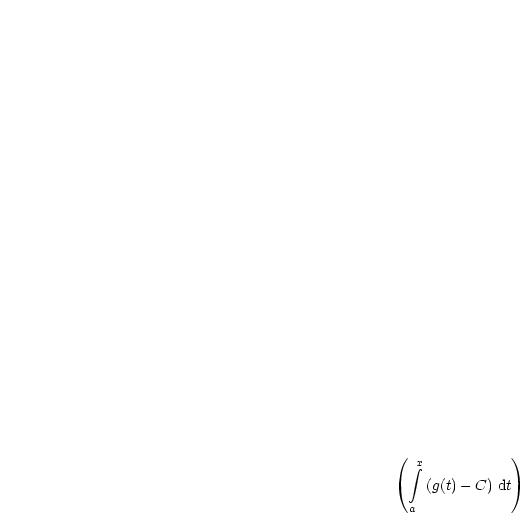 Es sei
Es sei ![]()
![]()
![]() 0:
0:
![]()
![]() C1[a,b],
C1[a,b], ![]() (a) = 0,
(a) = 0, ![]() (b) = 0. Wir benötigen außerdem:
(b) = 0. Wir benötigen außerdem:

Die Voraussetzung liefert nun:


Daraus folgt dann ![]() '(x) = 0
'(x) = 0 ![]() x und damit:
x und damit:

f, g ![]() C0[a,b]. Es gelte
C0[a,b]. Es gelte ![]() ab
ab![]() dx = 0
dx = 0 ![]() h
h ![]()
![]() 0. Dann gilt
(x) = g'(x)
0. Dann gilt
(x) = g'(x) ![]() x
x ![]() [a,b].
[a,b].
Es sei u(x) die Stammfunktion von f(t):

Damit folgt dann durch partielle Integration:

Also gilt weiterhin:
![|_ _|
integral b integral b integral x
[f(x)h(x)+ g(x)h'(x)] dx = |_ g(x)- f(t)dt _| h'(x)dx = 0 A h (- D0
a a a
------0 -------
(- C [a,b]](ma140x.gif)
Mit Satz 1 folgt dann:

Es sei f ![]() C0[a,b] und es gelte
C0[a,b] und es gelte ![]() abf(x)h(x)dx = 0
abf(x)h(x)dx = 0 ![]() h
h ![]()
![]() 0. Dann gilt f = 0.
Beweisen kann man dies, indem man in der Folgerung 1 g = 0 setzt.
0. Dann gilt f = 0.
Beweisen kann man dies, indem man in der Folgerung 1 g = 0 setzt.
![|------------------------------------------------------------------------------------------|
| { }|
|Esseif (- C0[a,b]undm (- N. Weiterhin seiD(m0) = y (- Cm[a, b] |h(k)(a) = h(k)(b) = 0, k = 0, 1, 2, ..., m
| integral b |
| (m) |
|gegeben. Es gelte f(x)h(x)dx = 0 A h (- D 0 . Die Behauptung ist nun, daßf (x) = 0 A x (- [a,b].
| a |
--------------------------------------------------------------------------------------------](ma142x.gif)
Aus Satz 2 erhalten wir Folgerung 2.
Wir wissen:


Mit Satz 2 folgt dann f = 0.
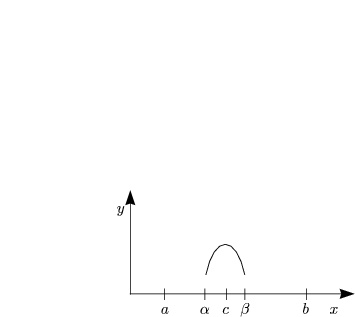
Wir nehmen an, daß f![]() 0. Daraus folgt dann f(c) > 0 für ein C
0. Daraus folgt dann f(c) > 0 für ein C ![]() (a,b). Es
gibt ein Intervall [
(a,b). Es
gibt ein Intervall [![]() ,
,![]() ]
] ![]() (a,b) mit f(x) > 0 für x
(a,b) mit f(x) > 0 für x ![]() [
[![]() ,
,![]() ] und stetigem f.
Wähle:
] und stetigem f.
Wähle:
![m (m)
{ [(x- a)(b - x)] (- D 0
~h(x) =
0 f¨ur x < a, x > b](ma147x.gif)
Setze dies nun in die Voraussetzung ein:

Dabei handelt es sich um einen Widerspruch.
F(y) = ![]() aby'(x)2 dx wird eindeutig auf D = {<
aby'(x)2 dx wird eindeutig auf D = {<![]() C1[a,b],y(a) = y
1,y(b) = y2}
durch y(x) minimiert:
C1[a,b],y(a) = y
1,y(b) = y2}
durch y(x) minimiert:
Dann soll ![]() (y) Minimum auf
(y) Minimum auf ![]() werden:
werden:

Die Lösung ist: