6.2 Normierter Raum

Es sei Y ein Vektorraum mit folgenden Eigenschaften:

||x||> 0 x Y ; Gleichheit nur für x = 0
||x + y||<||x|| + ||y|| x, y Y
||x|| = ||||x|| x Y ,

Es sei y = C[a,b]. Dann unterscheidet man:

Integralnorm: $integral b ||y|| = |y(x)|dx I a$
Maximumsnorm: $||y|| = max |y(x)|fur x (- [a,b] 0 ¨$

(y, ||^.||) sei normiert. Y ist dann auch ein metrischer Raum, beispielsweise mit der Metrik d(x,y) := ||y - x||.

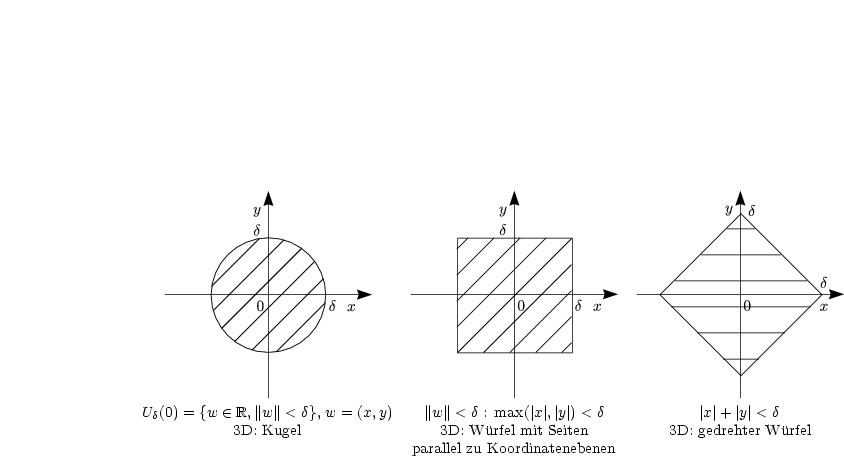
Sei a Y und > 0 gegeben. Dann definieren wir folgende Umgebung U mit dem Maß :

U (a) = {w (- Y |||w - a||< d} d

Diese nennt man -Umgebung von a. D Y heißt offen, falls es zu jedem a D ein > 0 gibt, so daß U(a) D ist.

Beispiel:

Betrachten wir den ⁿ. Die Elemente dieses Raumes sind n-Tupel von reellen Zahlen:

a = (a1,...,an) mit aj (- R

Dann kennen wir verschiedene Normen:

Euklidische Norm: $|_ _| 12 |_ _| 1p sum n 2 n sum p ||a||= |_ aj _| |_ |aj| _| , p > 1 j=1 j=1$
Maximumsnorm: $||a||= max{|aj| ,j = 1,...,n}$
||a|| = _j=1ⁿ|a_j|

Veranschaulichung von U(a) für n = 2 für i.), ii.) und iii.) (a = 0)

Ud(0) = {w (- R,||w|| < d}, w = (x,y) ||w|| < d : max (| x|,| y| ) < d |x|+ |y|< d
3D: Kugel 3D: Wu¨rfel mit Seiten 3D: gedrehter Wu¨rfel
parallel zu Koordinatenebenen

Beispiel:

Betrachten wir Y = [a,b], u: [a,b]

Integralnorm: $|_ _| 1 integral b p ||u|| = |_ |u(x)|pdx _| p > 1 a$
Besonders wichtig in der theoretischen Physik ist die L₂-Norm, also für p = 2. Man spricht von quadratintegrablen Funktionen. Wir beweisen zur Übung für den Fall p = 2 die Dreiecksungleichung: Die Behauptung ist also, daß gilt:
$1 1 1 |_ integral b _| 2 |_ integral b _| 2 |_ integral b _| 2 |_ |u(x)+ v(x)| 2dx _| < |_ |u(x)|2dx _| + |_ |v(x)| 2dx _| a a a$
Als erstes quadrieren wir die Ungleichung. Da alles > 0 ist, macht dies keine Probleme:
$1 1 integral b integral b integral b integral b integral b |_ integral b _ | 2 | _ integral b _| 2 u(x)2 dx+ v2(x)dx+2 |u(x)v(x)|dx < u(x)2 dx+ v2(x)dx+2 |_ u(x)2dx _| |_ v(x)2 dx _| a a a a a a a$
Jetzt fallen einige Terme heraus:
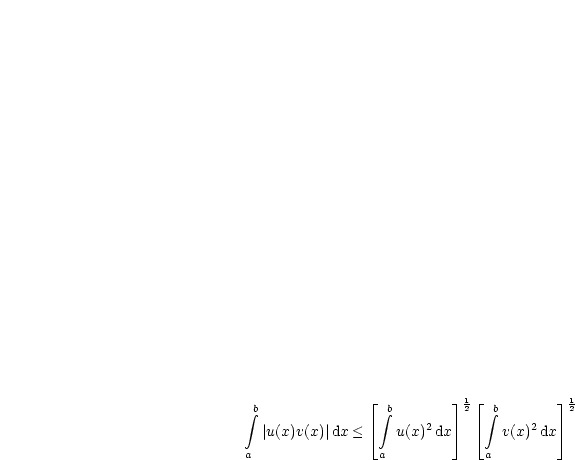
$|_ _ | 12 | _ _| 12 integral b integral b integral b |u(x)v(x)| dx < |_ u(x)2dx _| |_ v(x)2 dx _| a a a$

$integral b |u(x)| |v(x)| |_ --------- _| 12 |_ ------- _| -12 dx < 1 a integral b 2 integral b 2 |_ u(x) dx _| |_ v(x) dx _| a a$
Man hat also:
$integral b 2 integral b 2 f (x) dx = g(x) dx = 1 a a$
Damit erhalten wir folgendes Problem:
$integral b integral b integral b 2 2 Gilt f(x)g(x) dx < 1, wenn bekannt ist, daß f(x) dx = g(x) dx = 1? a a a$
Nun gilt allgemein nach den Binomischen Formel: ab <
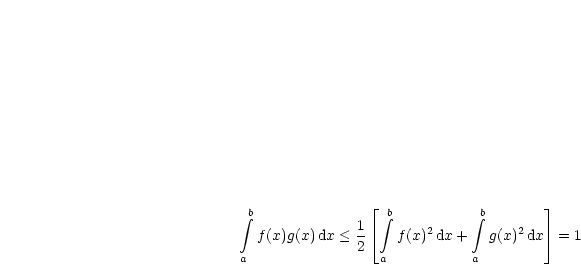
$| _ _| integral b integral b integral b f(x)g(x)dx < 1 |_ f(x)2 dx+ g(x)2dx _| = 1 a 2 a a$
Maximumsnorm: $||u||= max{|u(x)| ,a < x < b}$

Wir wollen nun auf dem Vektorraum der stetig differenzierbaren Funktionen Y = ¹[a,b] folgende Normen definieren:

Starke Norm: $||u ||0 = max {|u(x)| ,a < x < b}$

${ } U0d(w) = u (- C^1[a,b]|||u- w ||0 < d$
Man spricht hier auch von der starken -Umgebung.
Schwache Norm: $' ||u||1 = ||u||0 +||u ||0$

${ } U0d(w) = u (- C^1[a,b]|||u- w ||1 < d$
Diese wird als schwache -Umgebung bezeichnet.

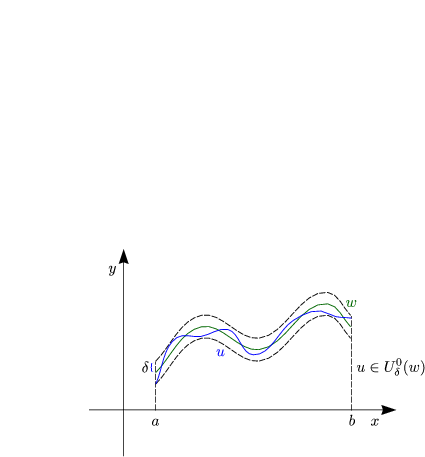
Man kann das ganze auch folgendermaßen veranschaulichen:

Aussage 1: U¹(w) U⁰(w) $u (- U1d(w) : ||u- w0|| + ||u'-w'||0 < d$
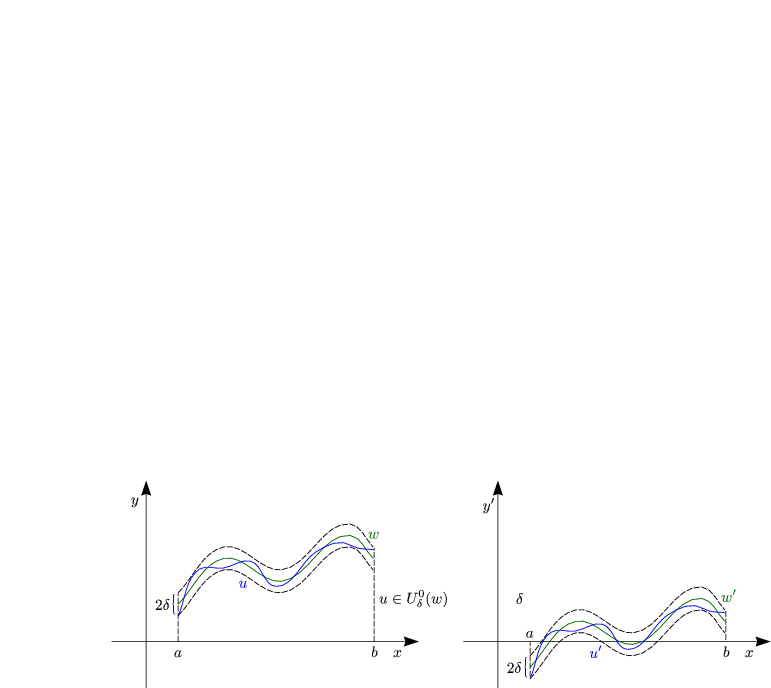
Daraus ergibt sich dann ||u - w₀|| < , also u U⁰(w).
Aussage 2: $(un) < Y, u (- Y$
Man hat eine Konvergenz bezüglich der starken und der schwachen Norm:
$un '--> u f¨ur n '--> oo in Y <==> ||un -u ||0 '--> 0 fu¨r n '--> oo$

$||un - u||1 '--> 0$
Es sei F: D Y . F heißt in y₀ Y stetig in x₀, falls gilt:
$( ) lim f(xn) = f lim xn = f(x0) n'--> oo n'-->o o$
Für jedes Folge x_nx₀ gilt f(x_n)f(x₀). F heißt stetig bezüglich der starken Norm [schwachen Norm], falls aus u_nu₀ bezüglich ||^.||₀ [||^.||₁] folgt, daß F(u_n)F(u₀) für n.
Aussage 3:
Ist F in u₀ bezüglich ||^.||₀ stetig, so ist F in u₀ auch bezüglich ||^.||₁ stetig.
Aussage 4:
Die Umkehrung bei Aussage 3 gilt nicht. Aus Aussage 2 ist bekannt:

Beweis von Aussage 2:
- Aus ||u₁ - u₀||₀0 für n folgt, daß F(u_n)F(u₀) für n. Wir wollen zeigen:
- Aus ||u_n - u₀||₀ + ||u_n'- u₀'||₀0 für n folgt F(u_n)F(u₀) für n.
Mit ||u_n - u₀||₀0 folgt aus 1.) die Behauptung.

Beweis von Aussage 3:

Wir machen ein Gegenbeispiel. Wir wählen ein Funktional, welches nur Ableitungen enthält:
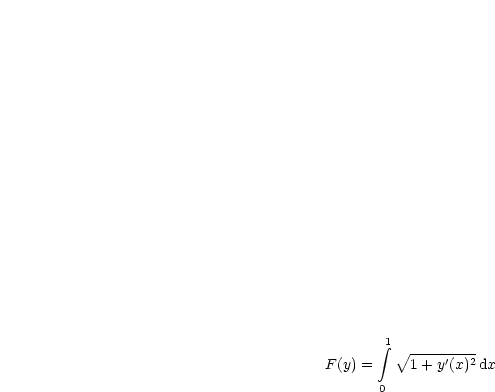
$integral 1 V~ -------- F(y) = 1 + y'(x)2dx 0$
- F ist auf ¹[a,b] stetig bezüglich der ||^.||₁-Norm.
  Zu zeigen ist, daß aus y_ny₀ in ||^.||₁-Norm folgt: F(y_n)F(y₀).
  $' ' ||yn- y0||+ ||yn- y0||'--> 0 f¨ur n '--> oo$
  
  $' ' ' ' ||yn- y0||0 = ma[ax,b]|yn(x)- y0(x)|'--> 0 f¨ur n '--> oo$
  Wenn dies in diesem Sinne konvergiert, dann liegt gleichmäßige Konvergenz vor und wir können Grenzwert und Integration vertauschen:
  $integral 1 V~ ------- integral 1 V~ --------- lim F (yn) = lim 1+ y'n(x)dx = lim 1 + y'(x)2dx = F(y0) n'--> oo n'--> oo 0 0 n'-->o o$
  F ist also stetig bezüglich der ||^.||₁-Norm.
- F ist jedoch nicht stetig bezüglich der ||^.||₀-Norm.
  Setze dazu y_n(x) = sin(n²x) y₀(x) = gleichmäßig auf dem Intervall [0,1], das heißt ||y_n -0||₀0 für n. Wäre F bezüglich der ||^.||₀-Norm stetig, so müßte gelten F(y_n)F(y₀ = 0) = 1. Hier gilt aber:
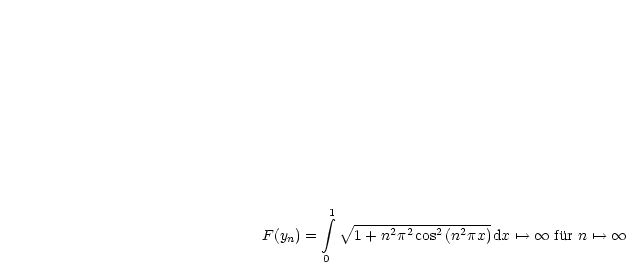
  $integral 1 V~ ----------------- F(yn) = 1 + n2p2cos2(n2px) dx '--> oo f¨ur n '--> oo 0$
  Damit ist das Funktional nicht stetig bezüglich der ||^.||₀-Norm.
Definition:

$|----------------------------------------------------------------------------------------| | | |Es sei F: D < Y '--> R, wobei C^1[a,b]. Gibt es ein u (- D und ein d > 0 mit | | F (u) < F(v) A v (- D /~\ U0d(u) starke | |{ } { } | | F (u) < F(v) A v (- D /~\ U1d(u) , so heiß t u schwache Minimalfunktion von F. F (u) ist | | | | starkes | |{ } | | schwaches relatives (lokales) Minimum f¨ur F auf D. | | | | | -----------------------------------------------------------------------------------------$
Aussage 5:
Jedes starke lokale Minimum ist auch schwaches lokales Minimum, aber nicht umgekehrt.

Beweis von Aussage 5:

Die Voraussetzung ist F(u) < F(v) v D $/~\$ U⁰(u). Wir behaupten, daß F(u) < F(v) v D $/~\$ U¹(u). Mit Aussage 1 gilt dies, da U¹(u) U⁰(u).
Die Voraussetzung ist F(u) < F(v) v D $/~\$ U¹(u). Dann behaupten wir, daß F(u) < F(v) v D $/~\$ U⁰(u) im allgemeinen nicht gilt!

Die starke Norm ist definiert durch:

||y|| = ||y ||+ ||y'|| = max {|y(x)|+ |y'(x)|,a < x < b} 1 0 0

Für > 0 können wir die starke -Umgebung von y mit y ¹[a,b] definieren:

{ } U 0d(y) = v (- C^1[a,b]|||y- v||0 < d

Dann können wir auch eine schwache -Umgebung definieren:

U 1(y) = {v (- C^1[a,b]|||y- v|| < d} d 1

Uns interessiert jetzt hauptsächlich die Minimumfunktion. F(y) ist schwaches [starkes] lokales Minimum, falls es ein > 0 gilt mit F(y) < F(v) v D $/~\$ U¹(y) $( 0 ) v (- D /~\ Ud(y)$ .

Beispiel:

integral 1 { } F(y) = (y'(x)2 + y'(x)3)dx, D = y (- C^1[0,1]| y(0) = y(1) = 0 0

y' ist das, was die starke von der schwachen Norm unterscheidet.

y(x) = 0 ist lokales schwaches Minimum von F auf D.
Betrachten wir die Definition. Es sei v U₁¹(0), das heißt, ||v - 0||₁ = ||v||₀ + ||v'||₀ < 1. Hieraus folgt ||v'||₀ < 1 und damit |v'(x)| < max_[0,1]|v'(x)| < 1 x [0,1]. Daraus ergibt sich dann -1 < v'(x) < 1 und somit v'(x) + 1 > 0 x [0,1]. Betrachten wir den Integranden:
$v'(x)2 + v'(x)3 = v'(x)2[v'(x) +1]> 0 >0 >0$
Daraus resultiert:
$F(v) > F (0) = 0 A v (- U 11(0)$
y(x) = 0 ist nicht lokales starkes Minimum von F auf D.
Zu jedem > 0 gibt es v U⁰(0) mit F(v) < F(0) = 0. Betrachten wir für 0 < p < 1 und q > 0:
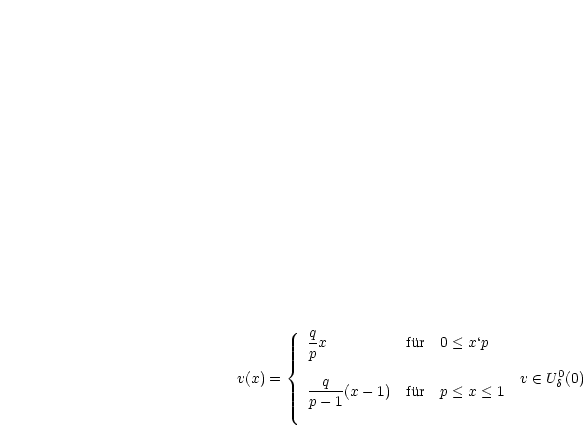
$q -x f¨ur 0 < x‘p { p v(x) = -q--- v (- U 0d(0) p- 1(x- 1) f¨ur p < x < 1$

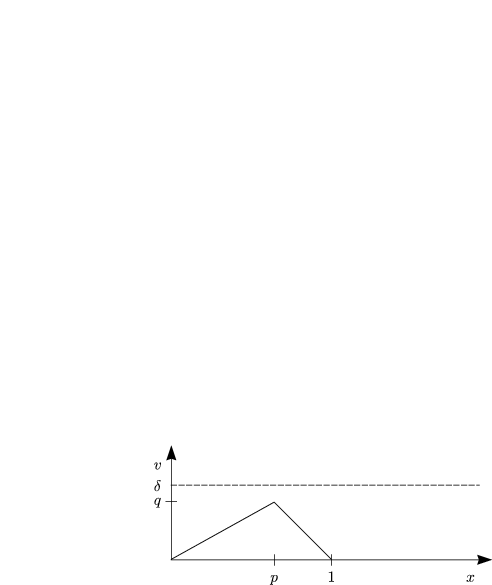
$integral 1 2 ( ) 2 ( ) F (v) = [v'(x)2 + v'(x)3]dx = q 1 + q + -p--- 1- -q--- 0 p p 1- p 1- p$

$lpim'-->1F (v) = - oo$
Es gibt damit ein p₀ mit p₀ < p < 1 und F(v) < 0 für diese p.

Satz:

|----------------------------------------------------------------------------------------|
| |
|Jede notwendige Bedingung f¨ur ein schwaches lokales Minimum ist eine notwendige Bedingung f¨ur starkes
|lokales Minimum. |
-----------------------------------------------------------------------------------------

Im folgenden werden wir uns einige Hilfssätze notieren.

Hilfssatz 1:

|----------------------------------------------------------------------------------------|
| integral x |
|F¨ur y (- ^C1[a,b] gilt: y(x) = y(a) + y'(t)dt, a < x < b |
| |
| a |
|Seien c1, ..., cN (- [a,b] die Unstetigkeiten von y'(die Ecken von y). Setze c0 = a und cN+1 = b. Sei
|x (- [a,b] beliebig fest. Damit liegt x im Intervall [ck,ck+1]. |
| |
| integral x N -1 integral x k-1 c integral j+1 |
| y'(t)dt = y(x)- y(a) = y(X) - y(c)+ sum [y(c )- y(c)] = y'(t)dt+ sum y'(t)dt |
| k j=0 j+1 j j=0 |
|a ck cj |
-----------------------------------------------------------------------------------------

Hilfssatz 2:

-----------------------------------------------------------------------------------------
| |
| integral x |
|Es sei h (- C^[a,b] und y(x) = h(t)dt, dann gilt y (- C^1[a,b] und y'(x) = h(x) f¨ur die x, in denen h|
| a |
|stetig ist. |
-----------------------------------------------------------------------------------------

Machen wir uns das ganze anschaulich ohne Beweis klar.

Liegt der x-Wert rechts von c, so folgt:

integral c integral x y(x) = h(t)dt+ h(t)dt a c

Es ist y'(x) = h(x) für x ein Stetigkeitspunkt. Was ist y'(c)?

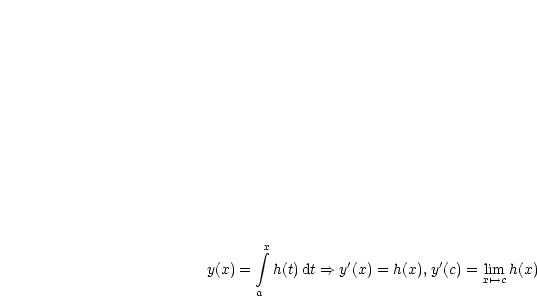
integral x y(x) = h(t)dt ==> y'(x) = h(x), y'(c) = xli'-->mc h(x) a

Hilfssatz 3:

|----------------------------------------------------------------------------------------|
| |
| integral b |
| a.) Aus y'(x)2dx = 0 folgt y'= 0 auf [a,b]. |
| |
| a |
| b.) Aus y'(x) = 0 mit x ± ck folgt, y(x) = const.auf [a,b]. |
-----------------------------------------------------------------------------------------|

Beweis für a.)

Es gilt y'(x)² > 0 und '² [a,b]. Daraus ergibt sich, daß folgendes Integral existiert:

b integral ' 2 y (x) dx a

integral b N ck integral +1 ' 2 sum ' 2 0 = y (x) dx = j=0 y(x) dx (c0 = a, cN+1 = b) a ck

Daraus ergibt sich dann:

ck integral +1 y'(x)2dx = 0 f¨ur k = 0, ..., N ck

Und hieraus ergibt sich wiederum y'(x) = 0 für c_k < x < c_k+1.

Beweis für b.)

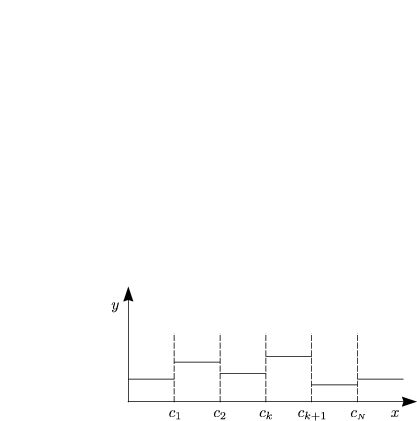
Es gilt ja nun y'(x) = 0 für x_k < x < c_k+1. Da y(x) stetig ist, folgt, daß y(x) = const. für a < x < b. Hier ist auch eine Argumentation mit dem Hilfssatz möglich.