6.3 1.Euler-Gleichung/Gleichung von du Bois-Reymond

6.3 1.EULER-Gleichung/Gleichung von DU BOIS-REYMOND

Satz 1:

Hierbei handelt es sich um eine notwendige Bedingung für ein schwaches relatives Minimum.

|----------------------------------------------------------------------------------------|
| ^1 |
|F¨ur y (- C [a,b] sei F integral (xy0) ein schwaches relatives Minimum. Dann gibt es eine Konstante c (- R, so daß
|f (x,y (x),y'(x)) = f (t,y (t),y'(t))dt+ c |
| p 0 0 z 0 0 |
| a |
|erfullt ist fur jedes x (- [a,b], fur das y'stetig ist. |
| ¨ ¨ ¨ 0 |
-----------------------------------------------------------------------------------------

Bemerkung:

Ist y₀ ⁿ, so bedeutet:

( ) ( ) fp1 fz1 fp2 fz2 fp = ... , fz = ... f f pn zn

Beweis:

Es ist die Frage, ob folgender Grenzwert existiert:

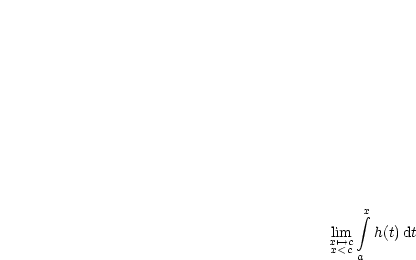
x integral lxim'-->c h(t)dt x<c a

Dies schätzen wir ab:

integral x integral c integral x || h(t)- h(t)dt|| = Bigl| h(t)dx||< max |h(t)||c- x|= const..|c- x| | | | [x,c] a a c

Wenn man nun den Grenzwert xc bildet, so ergibt sich 0, da max|h(t)| = const. ist.

Beweis:

Betrachte y(x) = y₀(x) + v(x), wobei v0 eine beliebige Funktion aus ¹[a,b] ist mit v(a) = v(b) = 0 und dem reellen Parameter . Wähle für > 0 gemäß | < . Dann gilt ||y - y₀||₁ = ||v||₁ = ||||v||₁ < . Das heißt, die y liegen in U¹(y₀). Nach Voraussetzung y₀ gibt es ein > 0 mit F(y₀) < F(y) y U¹(y₀). Nimm dieses , welches nach Voraussetzung gegeben ist, und die y = y₀ + v mit || < . Für diese y gilt also F(y₀) < F(y) = F(y₀ + v) = (). Daraus folgt dann, daß '(0) gleich Null sein muß:

integral b f'(0) = 0 = dF(y0;v) = [fz(x,y0(x),y0'(x))v(x) + fp(x,y0(x),y'0(x))v'(x)] dx a

Setze (x) = _a^xf_z(t,y₀(t),y₀'(t))dt [a,b] mit (a) = 0 und '(x) = f_z(x,y₀(x),y₀'(x)) dort, wo y₀' stetig ist.

(x(x))'= fzv(x)+ x(x)v'(x)

|_ _| ' integral b |_ x(x)v(x) _| dx = x(b)v(b)- x(a)v(a) = 0 a

Es gilt damit:

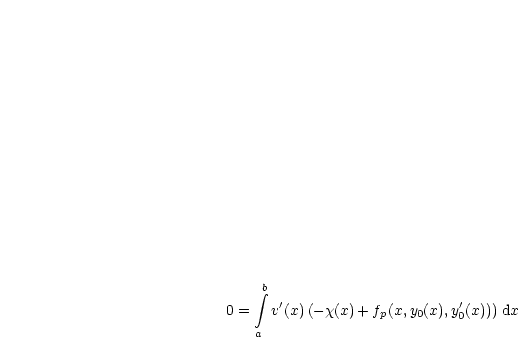
integral b 0 = v'(x)(- x(x)+ fp(x,y0(x),y'0(x))) dx a

Dies gilt für alle v ¹2[a,b] mit v(a) = v(b) = 0. Nach Hilfssatz 4 folgt dann, daß der Klammerausdruck eine Konstante ist:

|----------------------------------------| | integral x | |fp(x,y0(x),y'0(x)) = fz(t,y0(t),y0'(t))dt+ C | | a | -----------------------------------------

Bemerkungen:

Ist stückweise stetig, so wird [a,b] in Intervalle eingeteilt:

c c integral b ' integral 1 integral 2 integral b (xv) dx = + + ...+ a a c1 cN

Folgerung 1:

Wir die lokale schwache minimierende Kurve K₀ durch y = y₀(x) beschrieben, so gilt zwischen zwei Ecken von K₀ die 1.EULERgleichung in Differentialform:
$|-----------------------------------| | d ' ' | |dx-fp(x,y0(x),y0(x)) = fz(x,y0(x),y0(x)) -------------------------------------$
Diese Gleichung trat bisher im Zusammenhang mit konvexen Problem auf.
Folgerung 2: $integral x fz(t,y0(t),y'0(t))dt a$
Es gilt f_z , womit das Integral insgesamt stetig ist auf [a,b]. Damit ist f_p(x,y₀(x),y₀'(x)) stetig in Eckpunkten von K₀. Diese können charakterisiert werden durch (c,y₀(c)) mit p_-y₀'(c-)y₀'(c+) = p₊. Dies bedeutet:
$|---------------------------| -fp(c,y0(c),p-)-=-fp(c,y0(c),p+)-$
Man bezeichnet auch f_p(x,y₀(x),y₀'(x)) als U(x,y(x),y'(x)).

[next] [prev] [prev-tail] [front] [up]