6.4 1.Weierstrass-Erdmannsche-Eckenbedingung

[next] [prev] [prev-tail] [tail] [up]

6.4 1.WEIERSTRASS-ERDMANNsche-Eckenbedingung

Satz 2:

Als Voraussetzung gelte Satz 1.

|----------------------------------------------------------------------------------------|
|Es sei c (- (a,b), wobei (c,y (c)) eine Ecke von K : y = y (x) mit p = y'(c-), p = y'(c+). |
|Dann gilt U (c,y (c),p ) = 0U(c,y(c),p ) (WEIERS0TRASS -ER0DMANN 1),-wobe0i U(x,y(+x),y'(0x)) := |
|f (x,y(x),y'(x))0. - 0 + |
| p |
-----------------------------------------------------------------------------------------

Bemerkungen:

Existiert f_pp(c,y₀(c),t) für t zwischen p_-, p₊ und ist für diese t stetig, so gibt es ein zwischen p_- und p₊.

(Falls f_pp stets 0 ist, so kann die Lösungskurve keine Ecken haben.

Beispiel:

Betrachten wir folgendes Funktional:

integral b F (y) = g(x,y(x)) V~ 1-+-y'2(x)dx a

Wir berechnen die Minimalzeit, die das Licht vom Punkt y(a) nach y(b) benötigt. g(x,y(x)) sei der Brechungsindex des Materials.

V~ ------ f(x,z,p) = g(x,z) 1+ p2

fp = g(x,z) V~ -p--- 1+ p2

Notieren wir die Eckenbedingung:

--p----- ---p+--- g(c,y0(c)) V~ ----2-= g(c,y0(c)) V~ -----2 1+ p- 1 + p+

2 2 2 2 p- (1+ p+) = p+(1+ p- )

Durch Umformen erhalten wir hieraus die Bedingung p_-² = p₊² und damit p₊ = ±p_-. Im Falle p₊ = p_- liegen keinerlei Ecken vor. Durch Einsetzen von p₊ = -p_- in obige Gleichung erkennen wir, daß diese Bedingung nicht in Frage kommt.

Satz 3:

Voraussetzungen hierfür ist wieder Satz 1.

|----------------------------------------------------------------------------------------|
| integral x |
| ' ' ' ' |
|Es gilt f(x,y0(x),y0(x)) - y0(x)fp(x,y0(x),y0(x)) = fx(t,y0(t),y0(t))dt + C mit C = const.f¨ur alle |
| ' a |
|x (- [a,b], in denen y0(x) stetig ist. |
-----------------------------------------------------------------------------------------

Beweis:

Es sei K₀ = y = y₀(x) die minimierende Kurve. K₀ werde parametrisiert mit x = t und y = y₀(t) und a < x < b. K₀ wird variiert wie folgt: Wir bilden x = t + (t) mit y = y₀(t), a < t < b und kleinem || ( ¹[a,b], (a) = (b) = 0). Die K liegen für ||< ₀ (klein) in einer schwachen -Umgebung von K₀. (K lassen sich in der Form y = y(x) darstellen.) Wir müssen also x nach t auflösen können und dies ist der Fall, wenn (t)0 ist.

x˙(t) = 1+ a ˙c(t) > 0 f¨ur|a|< a0 gen¨ugend klein

Wir bilden damit (F(K) =)() = _a^bf und differenzieren nach :

integral b[ ( )] f'(0) = ˙c(t)f(t,y0(t), ˙y0(t))+ fx(t,y0(t), ˙y0(t))c(t) +fp(t,y0(t),y ˙0(t)) -˙c(t)y˙0(t) dt = a integral b [˙ ] = c(t)(f(t,y0(t),y˙0(t))- y˙0(t)fp(t,y0(t), ˙y0(t)))+ c(t)fx(t,y0(t), ˙y0(t)) dt a

(6.1)

integral b[ ] ˙ch(t) +c(t)fx(t,y0(t), ˙y0(t)) dt a

Wir setzen:

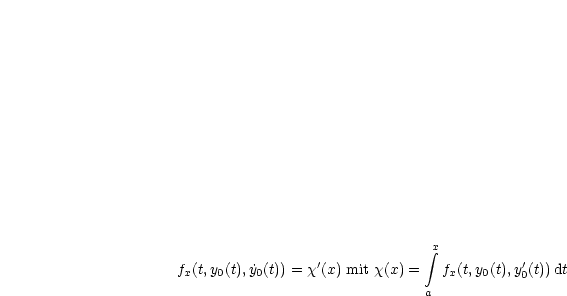
integral x fx(t,y0(t),y˙0(t)) = x'(x) mit x(x) = fx(t,y0(t),y'0(t))dt a

integral b ' ^ [h(x)v(x)+ g(x)v (x)] dx = 0 f¨ur v (- C[a,b] und v(a) = v(b) = 0 a

h(x) und g(x) sind stückweise stetig, also . Wir bringen „künstlich“ eine Ableitung auf h(x):

' x (x) = h(x)

integral x x(x) = h(t)dt a

Wir betrachten hierzu:

integral b integral b integral b (xv)'(x)dx = 0 = h(x)v(x)dx+ x(x)v'(x)dx a a a

b x integral ' Hilfssatz (Z15) integral 0 = [(g(x)- x(x))v (x)] dx -----------> g(x) = h(t)dt +C a 0

Satz 1:
Es galt hier g(x) = f_p(x,y₀(x),y₀'(x) und h(x) = f_z(x,y₀(x),y₀'(x).
Satz 3:
Hier hatten wir die Bezeichnungen = v und t = x.
$g(x) = f(x,y0(x),y'(x))- y'(x)fp(x,y0(x),y'(x)) 0 0 0$

$h(x) = fx(x,y0(x),y'0(x))$

Satz 3:

|----------------------------------------------------------------------------------------|
| x |
| ' ' ' integral ' ' |
|Es gilt f(x,y0(x),y0(x)) -y0(x)fp(x,y0(x),y0(x)) = fx(t,y0(t),y0(t))dt +C =: U (x,y0(x),y0(x)) |
| ' a |
|(E2) f¨ur alle x, in denen y0(x) stetig ist. |
-----------------------------------------------------------------------------------------

K₀ sei die durch y = y₀(x) für a < x < b beschriebene Kurve. Unstetigkeiten von y₀'(x) sind Ecken von K₀. Es sei (c,y₀(c)) ein eine Ecke, das heißt, y₀'(c-)y₀'(c+) (p_-p₊).

Folgerung 1:

Zwischen zwei Ecken von K₀ gilt Gleichung (E2) in differenzierter Form, also:

d --U(x,y0(x),y'0(x)) = fx(x,y0(x),y'0(x)) dx

Diese Differentialgleichung ist von der Form von E1:

d-f (x,y (x),y'(x)) = f (x,y(x),y'(x)) dx p 0 0 z 0 0

[next] [prev] [prev-tail] [front] [up]