

Wir erinnern uns an die 1.Eckenbedingung:
Daraus ergab sich dann für ein ![]() zwischen p+ und p-, daß fpp(c,y0(c),
zwischen p+ und p-, daß fpp(c,y0(c),![]() ) = 0 ist.
Wir können nun folgende Integration ausführen:
) = 0 ist.
Wir können nun folgende Integration ausführen:

Wir können aufschreiben:
Mit fp(c,y0(c),p+) = fp(c,y0(c),p-) erhalten wir dann:
Es handelt sich um eine Funktion von vier Veränderlichen:
Damit kann also der Ausdruck f(c,y0(c),p+)-f(c,y0(c),p-)-(p+ -p-)fp(c,y0(c),p-) geschrieben werden als:
An einer Ecke, in welcher die minimierende Kurve mit den Steigungen p- und p+ einläuft, gilt diese Beziehung. Nach dem Mittelwertsatz der Differentialrechnung gilt:
q liegt hier zwischen p+ und p-.
An einer Ecke gilt p+![]() p-. Mit der ersten WEIERSTRASS-ERDMANNschen
Eckenbedingung gilt:
p-. Mit der ersten WEIERSTRASS-ERDMANNschen
Eckenbedingung gilt:
Falls p- < p+, gilt p- < q < p+. Hieraus folgt fpp(c,y0(c),q1) = 0 mit p- < q1 < q. Für q < q2 < p+ gilt fpp(c,y0(c),q2) = 0.
Betrachten wir folgendes Funktional:
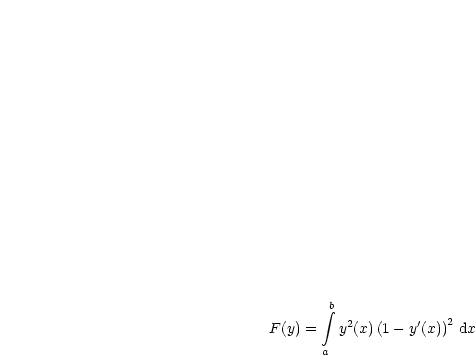
Hier gilt also f(x,z,p) = z2(1 - p)2. Weiterhin gilt fp = -2z2(1 - p), fpp = +2z2, also fpp(x,y(x),y'(x)) = -2y2(x). Wenn überhaupt Ecken bei Lösungen auftreten, dann müssen diese auf der x-Achse liegen.
Unser Integrant hängt nicht explizit von x ab. Damit folgt nach der Gleichung (E2):
Wir setzen u = y2 und damit u'(x) = 2yy'. Mit y2y'2 = ![]() u'2 ergibt sich
dann eine angenehmere Differentialgleichung:
u'2 ergibt sich
dann eine angenehmere Differentialgleichung:
Wir lösen nun nach u' auf und erhalten:
Wir haben nun wieder zwei Fälle:
Dann folgt hieraus durch Trennung der Veränderlichen un anschließende Integration:
Eine C1-Lösung der EULERschen Gleichung heißt Extremale (stationäre Funktion) des Funktionals F. Jede Kurve, welche aus Extremalen zusammengesetzt ist und die Eckenbedingung erfüllt, heißt gebrochene Extremale.
Fassen wir unsere Ergebnisse zusammen: Stationäre Funktionen sind:
Wir suchen stationäre Funktionen auf D1 = {y ![]() C1[-1,+1]|y(-1) = 0,y(1) = 1}.
Aus den Randbedingungen erhalten wir aus dem beiden ersten Lösungen
folgende Gleichungen:
C1[-1,+1]|y(-1) = 0,y(1) = 1}.
Aus den Randbedingungen erhalten wir aus dem beiden ersten Lösungen
folgende Gleichungen:
Daraus folgt C2 = ![]() und C3 = -
und C3 = -![]() 2.
2.
Es handelt sich um eine Hyperbel.

Es gilt x >![]() und x <-1 In D1 gibt es damit kein stationäre Funktionen. Wir
suchen deshalb gebrochene Extremale auf D2:
und x <-1 In D1 gibt es damit kein stationäre Funktionen. Wir
suchen deshalb gebrochene Extremale auf D2:
Deren Graphen können von folgende Form sein:
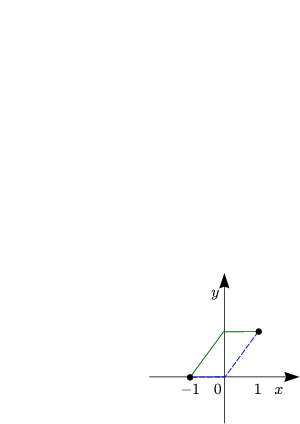
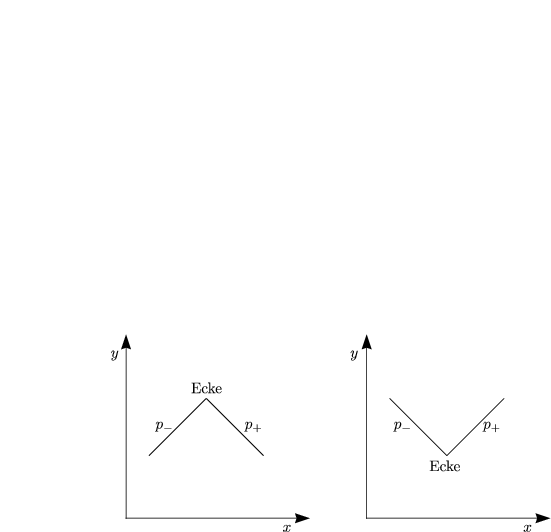
Eine Ecke bedeutet p+![]() p-. Aus der ersten Gleichung folgt dann, daß dies nur
dann gelten kann, wenn y02(c) = 0 ist. Damit ist dann automatisch auch die
zweite Bedingung erfüllt. Die gestrichelte Funktion ist gebrochenes Extremal.
Betrachten wir nun noch D3:
p-. Aus der ersten Gleichung folgt dann, daß dies nur
dann gelten kann, wenn y02(c) = 0 ist. Damit ist dann automatisch auch die
zweite Bedingung erfüllt. Die gestrichelte Funktion ist gebrochenes Extremal.
Betrachten wir nun noch D3:
Wir erhalten mittels der Randbedingungen:

Damit stelle dies eine Lösung ohne Ecken dar. Die Punkte (0,0) und (1,2) liegen auf demselben Hyperbelast.
Wiederholen wir nochmals die EULER-Gleichungen:
Falls y ![]()
![]() 2, dann folgt (E2) aus (E1). y sei C1-Lösung von E1:
2, dann folgt (E2) aus (E1). y sei C1-Lösung von E1:
Mittels (E1) folgt:
Dies ist die EULERsche Gleichung 2. Diese ist nützlich, wenn beispielsweise f nicht explizit von x abhängt:
Man bezeichnet dies dann als ein erstes Integral von (E1).
Wir hatten betrachtet:

Stationäre Funktionen sind:
In D1 gibt es keine C1 (C2)-Extremalen.
Aus den Eckenbedingungen hatten wir erhalten, daß eine Ecke für eine Extremale zwingend auf der x-Achse liegt.

Wir suchen nun Lösungen auf D3:
Durch Einsetzen der Randbedingungen in die allgemeine Hyperbelgleichung erhalten
wir y(x) = ![]() . Es handelt sich um eine zweimal stetige Lösung, um eine
glatte Extremale.
. Es handelt sich um eine zweimal stetige Lösung, um eine
glatte Extremale.
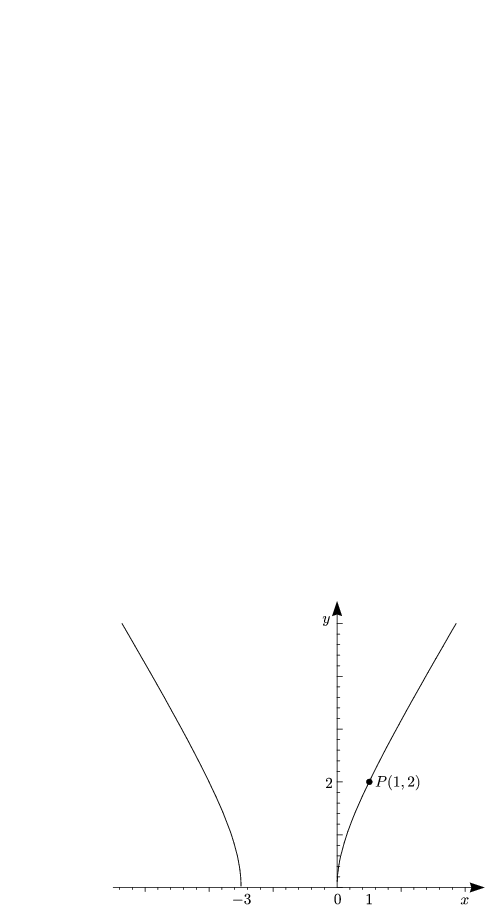
Hier erhält man gerade y(x) = 0, also auch hier eine Lösung ohne Ecken.
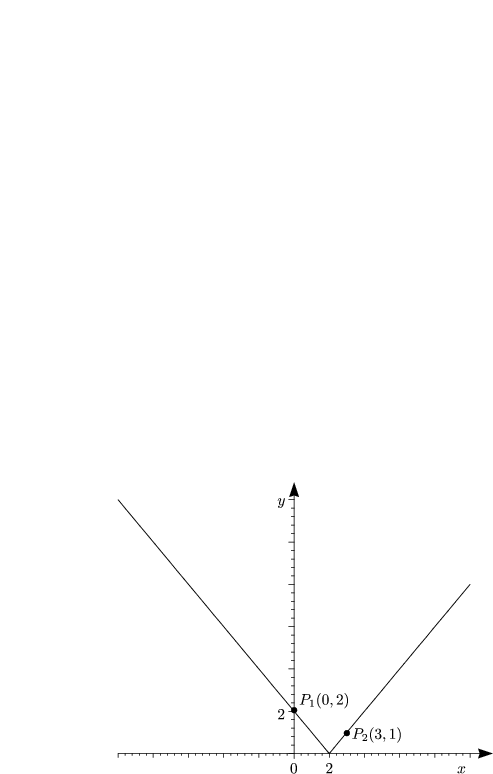
C2 und C3 werden mittels y(0) = 2 und y(3) = 1 bestimmt. Man erhält hier ein einfaches Gleichungssystem, welches wir hier nicht explizit lösen wollen. Man erhält dann daraus C2 = -2 und C3 = 0. Durch Einsetzen in die Hyperbelgleichung erhalten wir:
Durch Ziehen der Wurzel folgt, wobei für uns die positive Lösung wichtig ist:

Wir schauen uns folgendes Funktional an:
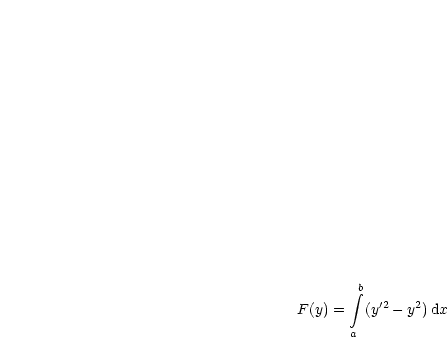
Wir erhalten wir dann f(x,z,p) = p2 - z2. Wir suchen nun Lösung der EULERschen Gleichung. Dazu benötigen wir außerdem fp = 2p, fz = -2z und fx = 0.
Wir notieren uns die Eckenbedingungen (Stetigkeit von fp). Wir erhalten hieraus p+ = px. Aus der Stetigkeit von U erhalten wir mit WE2: Diese beiden Gleichungen sind natürlich nur erfüllt für p+ = p-. Es gibt damit keine Extremalen mit Ecken; wir werden ale durch Lösen der EULERschen Gleichung nur stetig differenzierbare Funktionale finden:
Für die zweite EULERsche Gleichung gilt:
Wir erhalten aus der ersten Gleichung y'(x)(+y(x) = 0. Die Lösung dieser Differentialgleichung ist eine Linearkombination aus Sinus und Kosinusfunktionen:
Aus der zweiten EULERschen Gleichung erhalten wir y'2 + y2 = const..
Betrachten wir folgendes nicht so einfaches Beispiel

Daß die Funktion nur von der Ableitung y' abhängt, können wir sofort, sagen, da es sich bei den Extremalen um Geraden handelt. Wir rechnen dies nach:
Betrachten wir die erste EULERsche Gleichung:
Daraus ergibt sich 2y' + 3y'2 = C1 und damit durch Auflösen nach y' y' = C2, also:
Nun interessieren uns außerdem gebrochene Extremale. Die zu untersuchenden Eckenbedingungen sind hier nun nicht so einfach. Aus der ersten WEIERSTRASS-ERDMANNschen Eckenbedingung folgt:
Außerdem gilt nach der zweiten WEIERSTRASS-ERDMANNschen Eckenbedingung:
Dieses Gleichungssystem zu lösen, ist jetzt nicht so einfach. Auf jeden Fall ist
p+ = p- eine Lösung. Daraus folgen jedoch unsere zuvor berechneten C1-Funktionen.
Wir suchen jedoch Lösungen mit p+![]() p-.
p-.
Aus der ersten Gleichung erhalten wir nun p+ = -![]() und p+ = -
und p+ = -![]() . Da
beide Gleichungen gleichzeitig erfüllt sein müssen, ist p- = 0 nicht möglich
und außerdem auch p+ = 0. Ab jetzt können wir von p+
. Da
beide Gleichungen gleichzeitig erfüllt sein müssen, ist p- = 0 nicht möglich
und außerdem auch p+ = 0. Ab jetzt können wir von p+![]() 0 und p-
0 und p-![]() 0
(p+
0
(p+![]() p-) ausgehen. Damit können wir beide Gleichungen durcheinander
dividieren:
p-) ausgehen. Damit können wir beide Gleichungen durcheinander
dividieren:
Aus der ersten WEIERSTRASS-ERDMANNschen-Bedingung folgt p+ + p- = -![]() 3.
Durch Einsetzen in obige Gleichung folgt also wieder p+ = p-. Für Extremalen sind
Ecken damit nicht möglich.
3.
Durch Einsetzen in obige Gleichung folgt also wieder p+ = p-. Für Extremalen sind
Ecken damit nicht möglich.

Da das Funktional wieder nur von y' abhängt, können wir wieder sagen, daß es sich bei den Extremalen um Geraden handelt: y = cx + d.
Hier gilt f = (p2 - 1)2 und fp = 2 . 2p(p2 - 1). Damit erhalten wir U = f - pfp = (p2 - 1)(-3p2 - 1). Aus der ersten Eckenbedingung folgt:
Und aus der zweiten Eckenbedingung außerdem:
Wir suchen nun wieder Lösungen mit (p+,p-) mit p+![]() p-. Das Ergebnis ist also
p+ = 1, p- = -1 oder p+ = -1, p- = +1. Es können also Ecken auftreten un diese
müssen von folgender Form sein:
p-. Das Ergebnis ist also
p+ = 1, p- = -1 oder p+ = -1, p- = +1. Es können also Ecken auftreten un diese
müssen von folgender Form sein:
Schauen wir uns an, was dies für das konkrete Problem hier bedeutet:

Man erhält unendlich viele Lösungen. Jede gebrochene Funktion macht F zu Null, liefert also wirklich einen minimalen Wert.
Hier gibt es genau eine Lösung, nämlich y(x) = x.
Hier gibt es genau die Lösung y = ![]() x.
x.
Es gibt komplizierte Kriterien, einem Funktional anzusehen, daß es minimal wird. In den
ersten Kapiteln hatten wir das Konvexitätskriterium verwendet; dieses ist jedoch sehr
grob. Deshalb rechen wir nun direkt nach, daß für ![]() > b die Funktion y =
> b die Funktion y = ![]() x für
das Integral wirklich eine starke lokale minimierende Funktion darstellt.
Betrachten wir hierzu einfach benachbarte Kurven durch Einsetzen und
Vergleichen:
x für
das Integral wirklich eine starke lokale minimierende Funktion darstellt.
Betrachten wir hierzu einfach benachbarte Kurven durch Einsetzen und
Vergleichen:
Wir haben also benachbarte Funktionen konstruiert.
![( ) ( ) integral b |_ (( )2 )2 (( ) - )2_ |
F b-+ j(x) - F bx = |_ b-+ j'(x) - 1 - b- 1 _| dx =
b b b b
b [ 0 ] ( ) b
integral ( b ' ' 2)2 (b2 )( b ' ) b22 b integral '
= 2b-j(x)+ j (x) + 2 b2- 1 2-bj + j dx2 -b- -1 2-b j dx = 0
a 0](ma763x.gif) | (6.2) |
Es handelt sich um „stark“, da die Abschätzung unabhängig davon ist, ob ![]() ' groß
ausfällt. Wenn man eine Bedingung bekäme, daß die Abschätzung nur gilt, wenn
das
' groß
ausfällt. Wenn man eine Bedingung bekäme, daß die Abschätzung nur gilt, wenn
das ![]() ' in einer kleinen Schranke verläuft, dann hätte man eine schwache
Abschätzung.
' in einer kleinen Schranke verläuft, dann hätte man eine schwache
Abschätzung.