9.1 HAMILTON-Prinzip

Falls das System bestimmte Positionen zu den Zeiten t₀ und t₁ annimmt, dann bewegt es sich zwischen diesen Positionen während der Zeitspanne t₁ - t₀ längs solcher zulässiger Bahnkurven (Trajektorien) y = y(t), für die das Integral

stationär wird. y = y(t) heißt zulässig, falls gewisse k < 3n Nebenbedingungen, welche zu dem betrachteten System gehören, erfüllt sind. Zur Zeit t hat das System N = 3n - k Freiheitsgrade; das heißt, seine Lage zur Zeit t wird eindeutig durch N skalare Größen q₁(t), ..., q_N(t) beschrieben. Wir bezeichnen q(t) = ^N als Zustandsvektor, wobei N zeitunabhängig sein soll.

Voraussetzung:

y und q sollen eindeutig auseinander berechenbar sein. Wir haben also eine eindeutige Zuordnung y(t) = g(q(t)) g: ^N3n und y C¹. Für jeden einzelnen Massenpunkt gilt y_j(t) = g_j(q(t)) mit j = 1, ..., n und g_j: ^N3. Mittels der Kettenregel gilt:

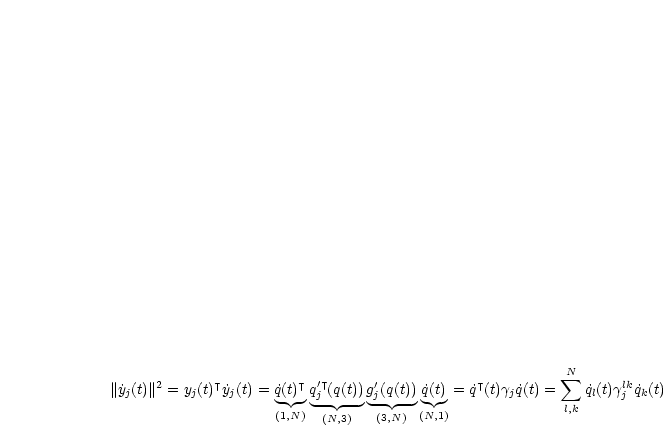
_j ist nun eine symmetrische (N,N)-Matrix mit (_j)_l,k=1,...,N^lk.

Damit erhalten wir einen Ausdruck für die kinetische Energie:

Führen wir die Summation über j aus, so bleibt ein Ausdruck abhängig von l und k übrig, den wir als A(a) = a_lk(q(t))_lk bezeichnen wollen, wobei es sich hier um eine symmetrische (N,N)-Matrix handelt.

Hierbei gilt (q(t),(t)) = ²(q(t),(t)) für > 0. Nach Satz 2 (Z 22) gilt 2(u,v) = v_v(u,v).

9.1.1 Ebenes starres Pendel

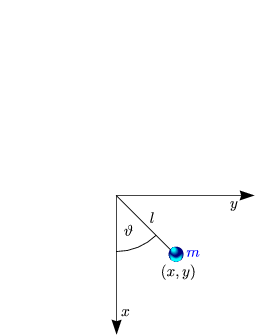
Hier ist n = 1 und N = 1. Damit gilt x(t) = l cos(t) und y(t) = l sin(t), womit wir (,) = l²² erhalten.

9.1.2 Kugelpendel

Ein Pendel bewege sich auf einer Kugel mit dem Radius l, womit Kugelkoordinaten günstig sind. Hier gilt n = 1 und N = 2; als unabhängige Koordinaten wählen wir die beiden Winkel und .

Es gilt nun:

Überprüfen wir die obige Beziehung:

Hiermit gilt

was so sein muß.

Zusammenfassung:

Ab jetzt setzen wir L^*L, T^*T und U^*U.

Dieses Funktional sei stationär (W(q;) = 0, (t₀) = (t₁) = 0). Die entsprechenden EULERgleichungen (LAGRANGEgleichungen) lauten:

Hierbei handelt es sich um N skalare Gleichungen.

9.1.3 Feder-Masse-Pendel

Wir wollen eine Transformation (x,0,x₁,y₁)(q₁,q₂) = (x,) durchführen. Für den Massenpunkt M gilt nun:

Auf m wirkt die Federkraft k(x) mit k(0) = 0.

Da für diese Matrix m+M > 0 und (m+M)Ml² -M²l² cos² = mMl² +M²l² sin² > 0 gilt, ist die Matrix regulär und damit invertierbar. Wir schreiben also die LAGRANGEfunktion hin:

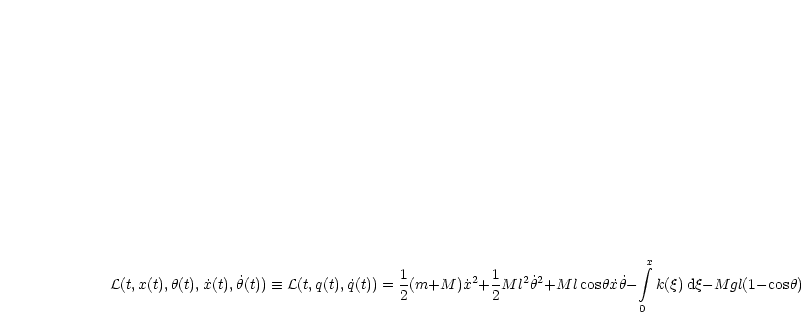
Daraus berechnen wir:

Nun können wir für die beiden EULERgleichungen ermitteln:

Führen wir die Differentiation auf der linken Seite von Gleichung (2) aus, so folgt:

Multiplizieren wir nun Gleichung (1) mit und subtrahieren diese von Gleichung (3), so folgt mit den Abkürzungen = und = (x):

Gesucht sind x = x(t) und = (t). Hierbei handelt es sich um ein gekoppeltes nichtlineares Differentialgleichungssystem 2.Ordnung. Ein System dieser Art ist schwer zu lösen. Deshalb führen wir für kleine Zeiten t eine Linearisierung durch, also cos()1, (x(t))x(t) (mit = const.) und sin.

Aus diesen beiden Gleichungen ergibt sich:

Hieraus folgt durch zweimaliges Differenzieren:

Durch Einsetzen der nach aufgelösten ersten Gleichung gilt nun:

Mit dem Ansatz x(t) = exp(t) erhält man ein Polynom 4.Grades, welches als Übung gelöst werden kann.

Bemerkung (Übung):

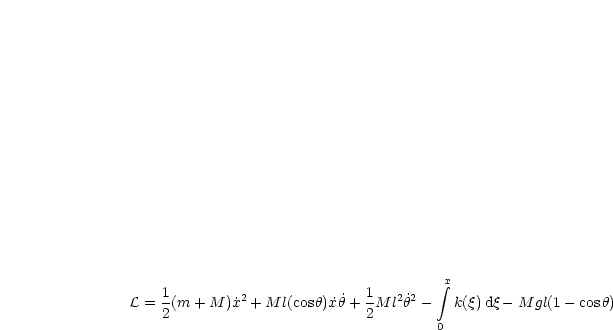
Linearisiere L. Dann sind die LAGRANGEgleichungen wieder die linearen Gleichungen für x, von oben. Achtung! Bei der zweiten Gleichung ist cos = 1 - + O(⁴) zu setzen!