
Gesucht ist ein Variationsintegral derart, daß die zugehörige EULERgleichungen gerade die zugehörigen HAMILTONgleichungen sind. Damit soll folgendes Funktional stationär werden:

Wir schreiben die EULERschen Gleichungen für
f(t,q(t),p(t),![]() (t),
(t),![]() (t)) =
(t)) = ![]() (t) . p(t) -H(t,q(t),p(t)) = v . w -H(t,u,w)
hin:
(t) . p(t) -H(t,q(t),p(t)) = v . w -H(t,u,w)
hin:

Hieraus ergibt sich dan weiter durch Einsetzen der ursprünglichen Variablen die HAMILTONschen Gleichungen:
Wir betrachten nun:

Auch hieraus ergibt sich also ![]() = -Hu und
= -Hu und ![]() = Hw.
= Hw.
![|----------------------------------------------------------------------------------------|
| |
| integral t1 |
|Die Extremalen von W1(q,p) = [˙q(t) .p(t)- H(t,q(t),p(t))] dt sind die L¨osungen der HAMILTONschen
| t0 |
| t integral 1 |
|Gleichungen f¨ur das Problem, daß W (q) = L(t,q(t),q˙(t))dt station¨ar werden soll. Dasselbe leistet das
| |
| integral t1 t0 |
| |
|Problem W2(q, p) = [-q(t) .˙p(t)- H(t,q(t),p(t))] dt. |
| t0 |
-----------------------------------------------------------------------------------------](ma1228x.gif)
Wir bilden also die Differenz der beiden Funktionale:
![t integral 1 integral t1 t integral 1[d ]
W1(q,p)-W2(q,p) = = [˙q(t).p(t)+ q(t).˙p(t)] dt = dt (q(t).p(t)) dt
t0 t0 t0](ma1229x.gif)
Die zugehörigen EULERgleichungen lauten:
Damit liefern die EULERschen Gleichungen keine Bedingungen.
![|----------------------------------------------------------------------------------------|
| |
| integral t1 integral t1 |
|F¨ur F (y) = -df (t,y(t))dt = [ft(t,y(t))+ fz(t,y(t)) .˙y(t)] dt (station¨ar) gilt: |
| t0 dt t0 |
| |
| |
| |
| • Die EULERgleichungen ergeben keine Bedingung fu¨r y; sie sind Identit¨aten, welche stets erf¨ullt sind.
| • dF (y,j) = 0, j(t0) = j(t1) = 0 ist f¨ur jedes y und jedes j erf¨ullt. |
| |
-----------------------------------------------------------------------------------------](ma1231x.gif)
![|
d- || d-
dF(y,j) = deF(y,+ej)|e=0 = de [f(t1,y(t1)+-ej(t1))- f(t0,y(t0)+-ej(t0))]e=0 = 0
unabh¨angig von e](ma1232x.gif)
Der letzte Ausdruck ist unabhängig von ![]() , womit die Ableitung gleich 0
ist.
, womit die Ableitung gleich 0
ist.

Es sei H = H(t,u,w) mit u ![]()
![]() N und w
N und w ![]()
![]() N seien gegeben. Für q = q(t), p = p(t)
gelten:
N seien gegeben. Für q = q(t), p = p(t)
gelten:
Gesucht ist eine Transformation (u,w) [![]() N ×
N × ![]() N]
N] ![]() (U,W) [
(U,W) [![]() N ×
N × ![]() N] und eine
Funktion H = H*(t,U,W) derart, daß für die mittels der Transformation aus
(q(t),p(t)) hervorgehenden Funktionen (Q(t),P(t)) die folgenden Gleichungen
gelten:
N] und eine
Funktion H = H*(t,U,W) derart, daß für die mittels der Transformation aus
(q(t),p(t)) hervorgehenden Funktionen (Q(t),P(t)) die folgenden Gleichungen
gelten:
Es sei p = ![]() (t,Q,P) und q =
(t,Q,P) und q = ![]() (t,Q,P):
(t,Q,P):
Vor vorher betrachten wir folgendes Funktional, welches stationär werden soll:
![integral t1
W (q,p) = [p.˙q- H(t,q,p)] dt
1
t0](ma1238x.gif)
Die zugehörigen EULERschen Gleichungen lauten ![]() (t) = Hw,
(t) = Hw, ![]() (t) = -Hu (für 2N
Funktionen).
(t) = -Hu (für 2N
Funktionen).
![t integral 1[ ]
W1(Q, P) = P .˙Q -H*(t,Q, P) dt
t
0](ma1241x.gif)
Hier lauten die EULERgleichungen ![]() (t) = HW* und
(t) = HW* und ![]() (t) = -HU* (für 2N
Funktionen). Wir wollen nun ein Problem für 4N Funktionen herleiten, indem wir
beide Funktionale voneinander subtrahieren:
(t) = -HU* (für 2N
Funktionen). Wir wollen nun ein Problem für 4N Funktionen herleiten, indem wir
beide Funktionale voneinander subtrahieren:
![integral t1[ ] t integral 1
W (q,p,Q, P) = (p .˙q- H) -(P .Q˙- H*) = f(t,q,p,Q,P,q˙, ˙p, ˙Q,P˙)dt
t0 t0](ma1244x.gif)
Für dieses Problem gelten dann alle EULERgleichungen der beiden einzelnen Probleme, also erhalten wir 4N Funktionen. Nun können wir noch einen zusätzlichen Term in Form einer totalen Zeitableitung addieren:
![integral t1[ d ]
W (q,p,Q,P ) = (p.q˙- H)- (P .Q˙- H*)+ dtF (t,q,p,Q,P ) dt
t0](ma1245x.gif)
Dies gilt für eine beliebige Funktion F = F(t,q,p,Q,P) von 4N + 1 Variablen. Nach den Vorbemerkungen hat das Variationsproblem mit dem Integranden
dieselben 4N EULERgleichungen. Angenommen, wir haben die gesuchte
Transformation p = ![]() (t,Q,P), q =
(t,Q,P), q = ![]() (t,Q,P). Hiermit können 2N Variablen in F
eliminiert werden, so daß F von 2N + 1 Variablen abhängt. F muß von einem Satz
alter und einem Satz neuer Variablen abhängen. Dafür gibt es die vier Möglichkeiten
F = F(t,q,Q), F = F(t,q,P), F = F(t,p,P) und schließlich F = F(t,p,Q). F
heißt Erzeugende Funktion der Transformation. Wir bestimmen F im Fall
F = F(t,q,P).
(t,Q,P). Hiermit können 2N Variablen in F
eliminiert werden, so daß F von 2N + 1 Variablen abhängt. F muß von einem Satz
alter und einem Satz neuer Variablen abhängen. Dafür gibt es die vier Möglichkeiten
F = F(t,q,Q), F = F(t,q,P), F = F(t,p,P) und schließlich F = F(t,p,Q). F
heißt Erzeugende Funktion der Transformation. Wir bestimmen F im Fall
F = F(t,q,P).
Hiermit folgt aus (*):
Diese Gleichung ist erfüllbar, falls Fq(t,q,P) = p, Fp(t,q,P) = Q und H* = H + Ft
gilt. Aus der zweiten Bedingung kann man q = ![]() (t,Q,P) bestimmen und damit folgt
aus der ersten Bedingung p =
(t,Q,P) bestimmen und damit folgt
aus der ersten Bedingung p = ![]() (t,Q,P). Betrachten wir schlußendlich noch die dritte
Bedingung, so erhalten wir:
(t,Q,P). Betrachten wir schlußendlich noch die dritte
Bedingung, so erhalten wir:
Die Idee ist nun folgende:

Dies bedeutet ![]() = Hp und
= Hp und ![]() = -Hq.
= -Hq.
Das Ziel ist nun ![]()
![]() =
= ![]()
![]() * = 0. Dazu machen wir den Ansatz
* = 0. Dazu machen wir den Ansatz ![]() (
(![]() -
-![]() * = 0 und dies
gilt, falls:
* = 0 und dies
gilt, falls:
Wir eliminieren in F zunächst 2N Variablen mittels der kanonischen Transformation, so daß F von t und einem Satz alter und einem Satz neuer Koordinaten abhängt: F = F(t,q,P), F(t,p,P) und F(t,q,Q). Wir verwenden den Fall F = F(t,p,P):
Dies ist äquivalent zu:
Wir definieren an dieser Stelle Q(t) := Fp(t,p(t),P(t) und hieraus folgt p(t) = ![]() (t,Q,P).
Außerdem setzen wir
(t,Q,P).
Außerdem setzen wir ![]() p(t)=
p(t)=![]() (t,Q,P) =
(t,Q,P) = ![]() (t,Q,P).
(t,Q,P).
Es sei F(t,q,P) = q . Pt (mit N = 1). Aus Q = Fp erhalten wir Q = qt
und damit q = ![]() (=
(= ![]() (t,Q,P). Aus p = Fq folgt p = Pt(=
(t,Q,P). Aus p = Fq folgt p = Pt(= ![]() (t,Q,P)) und
P =
(t,Q,P)) und
P = ![]() .
.
Als Voraussetzung verwenden wir ![]() = Hp(t,q,p) und
= Hp(t,q,p) und ![]() = -Hq(t,q,p) und
behaupten, daß
= -Hq(t,q,p) und
behaupten, daß ![]() = HP*(t,Q,P) und
= HP*(t,Q,P) und ![]() = -HQ*(t,Q,P).
= -HQ*(t,Q,P).
Kommen wir zurück zu F = F(t,q,P).
Eine Erzeugendenfunktion F = F(t,q,P), für die H*(t,Q,P) = 0 ![]() t, Q und P gilt,
heißt Wirkungsfunktion A(t,q,P). Aus H* = 0 ergibt sich
t, Q und P gilt,
heißt Wirkungsfunktion A(t,q,P). Aus H* = 0 ergibt sich ![]() (t) =
(t) = ![]() (t) = 0, also
Q(t) =
(t) = 0, also
Q(t) = ![]() (
(![]()
![]() N) und P(t) =
N) und P(t) = ![]() (
(![]()
![]() N), wobei
N), wobei ![]() ,
, ![]() konstant sind. Hieraus folgt
A = A(t,q,
konstant sind. Hieraus folgt
A = A(t,q,![]() ).
).
Dies ist die sogenannte Hamilton-Jacobi-Differentialgleichung. Hierbei handelt
es sich um eine partielle (im allgemeinen nichtlineare) Differentialgleichung
1.Ordnung für A. A = A(t,q,![]() ) sei die Lösung, die von N Konstanten
) sei die Lösung, die von N Konstanten ![]() 1,
1, ![]() 2, ...,
2, ..., ![]() N
abhängt. Aus F(t,q,P) erhalten wir Q = FP = AP = A
N
abhängt. Aus F(t,q,P) erhalten wir Q = FP = AP = A![]() =
= ![]() . A
. A![]() (t,q,
(t,q,![]() ) =
) = ![]() ist
eine implizite Darstellung für q = q(t) und ist abhängig von 2N Konstanten
ist
eine implizite Darstellung für q = q(t) und ist abhängig von 2N Konstanten ![]() 1, ...,
1, ...,
![]() N und
N und ![]() 1, ...,
1, ..., ![]() N.
N.
Betrachten wir das System der HAMILTONschen Gleichungen:
Gesucht sind x = x(t) ![]()
![]() n und y = y(t)
n und y = y(t) ![]()
![]() n. Betrachte die zugehörige
HAMILTON-JACOBI-Gleichung für eine Funktion S = S(t,x):
n. Betrachte die zugehörige
HAMILTON-JACOBI-Gleichung für eine Funktion S = S(t,x):
Wir begnügen uns mit der Voraussetzung H![]() C2(
C2(![]() ×
× ![]() n ×
n × ![]() n). S = S(t,x,a) sei
Lösung der HAMILTON-JACOBI-Gleichung, die noch von n Parametern a abhängt.
Das heißt für jedes a
n). S = S(t,x,a) sei
Lösung der HAMILTON-JACOBI-Gleichung, die noch von n Parametern a abhängt.
Das heißt für jedes a ![]() B
B ![]()
![]() n gelte St(t,x,a) + H(t,x,Sx(t,x,a)) = 0
(1). Des weiteren sei det(Sxjak)
n gelte St(t,x,a) + H(t,x,Sx(t,x,a)) = 0
(1). Des weiteren sei det(Sxjak)![]() 0 auf
0 auf ![]() ×
× ![]() n ×
n × ![]() n. Solch eine Lösung
bezeichnet man auch als vollständiges Integral. Dann gewinnt man aus den
Gleichungen
n. Solch eine Lösung
bezeichnet man auch als vollständiges Integral. Dann gewinnt man aus den
Gleichungen
mit beliebigen Parametern b = (b1,...,bn) eine 2n-parametrige Lösungsschar des HAMILTONschen Systems: x = X(t,a,b und y = Y (t,a,b).
Folgendes Funktion mit y = y(x) soll stationär werden:
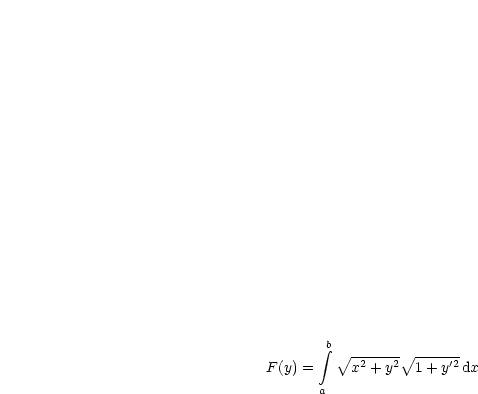
Gesucht ist S(x,y,a) ![]()
![]() mit Sx + H(x,y,Sy) = 0. Hier gilt also
Sx +
mit Sx + H(x,y,Sy) = 0. Hier gilt also
Sx + ![]() = 0.
= 0.
Man bezeichnet eine solche Differentialgleichung auch als Eikonalgleichung. Zur Lösung dieser partiellen Differentialgleichung machen wir den Separationsansatz S(x,y) = f(x) + g(y).
Wir erhalten die zwei gewöhnlichen Differentialgleichungen f'2(x) = x2 + a und g'(y)2 = y2 - a und damit:
Durch Auflösen nach y erhalten wir die gesuchten Extremalen:
Es handelt sich um eine implizite Lösungsdarstellung.
Wir differenzieren (1) nach a:
Anschließend differenzieren wir nach x:
Wir subtrahieren Gleichung (2) von (1)a:
Dies muß für alle k Summanden gelten, wobei vorausgesetzt wird, daß
die Determinante ![]() 0 ist.
0 ist.
Wir setzen voraus, daß alles in der Ebene stattfindet.

Die EULERgleichungen lauten:

Hieraus ergibt sich ![]() 1 = 0 und
1 = 0 und ![]() 2 = -g. Mit p1 = m
2 = -g. Mit p1 = m![]() 1,
1, ![]() 1 =
1 = ![]() und p2 = m
und p2 = m![]() 2,
2,
![]() 2 =
2 = ![]() erhalten wir:
erhalten wir:
Die HAMILTON-JACOBI-Gleichung lautet für S = S(t,x,a):
Wir machen eine Variablentrennung S = u(x1) + v(x2) + w(t) als Ansatz:
Wir bringen das, was nicht von t abhängig ist, auf die rechte Seite:
Wir erhalten also:
Als Lösung folgt:
S ergibt sich aus u + v + w. Der Satz sagt aus: „Bilde Sa1 = b1 und Sa2 = b2 und berechne hieraus x = x(t).“
Aus x1(0) = 0 folgt aus der ersten Gleichung b1 = 0 und aus der zweiten Gleichung
b2 = -![]() .
.
Das Problem findet wieder in einer Ebene statt:

Die Masse m2 soll in Ruhe sein. Gesucht ist die Bahnkurve von m1:

Mit U = -![]() und T =
und T = ![]() (
(![]() 12 +
12 + ![]() 22) ergibt sich:
22) ergibt sich:
Die HAMILTON-JACOBI-Gleichung lautet für S = S(t,x1,x2):
Wir bezeichnen ![]() =
= ![]() und nennen
und nennen ![]() wieder S mit
wieder S mit ![]() =
= ![]() 2:
2:
Wir führen Polarkoordinaten ein durch x1 = r cos![]() und x2 = r sin
und x2 = r sin![]() :
:
Mit ![]() r = Sx1 cos
r = Sx1 cos![]() + Sx2 sin
+ Sx2 sin![]() und
und ![]()
![]() = Sx1(-r sin
= Sx1(-r sin![]() ) + Sx2(r cos
) + Sx2(r cos![]() ) folgt:
) folgt:
Gesucht ist ![]() =
= ![]() (t,r,
(t,r,![]() ,a1,a2). Hier kann man nun den Separationsansatz
,a1,a2). Hier kann man nun den Separationsansatz
![]() =
= ![]() 1(t) +
1(t) + ![]() 2(
2(![]() ) +
) + ![]() 3(r) machen:
3(r) machen:
Hieraus ergibt sich ![]() 1(t) = a1t und weiter:
1(t) = a1t und weiter:
Hieraus folgt ![]() 2(
2(![]() ) = a2
) = a2![]() . Mit r0 = r(t0) für t > t0 folgt:
. Mit r0 = r(t0) für t > t0 folgt:


Nach unserem Satz von JACOBI setzen wir ![]() a1 = b1,
a1 = b1, ![]() a2 = b2 und bestimmen
hieraus r = r(t),
a2 = b2 und bestimmen
hieraus r = r(t), ![]() =
= ![]() (t):
(t):

Hierbei handelt es sich um eine Darstellung für r = r(t): das Weg-Zeit-Gesetz. Wir setzen:

Dies ist eine implizite Darstellung von r = r(![]() ), also der Bahnkurve. Mittels
BRONSTEIN folgt hieraus jetzt:
), also der Bahnkurve. Mittels
BRONSTEIN folgt hieraus jetzt:
