Ersetze durch 2N Gleichungen 1.Ordnung für q = q(t) ![]()
![]() N und p = p(t)
N und p = p(t) ![]()
![]() N
(verallgemeinerte Impulse). Die Idee ist dabei folgende:
N
(verallgemeinerte Impulse). Die Idee ist dabei folgende:
Betrachten wir dazu das Wirkungsfunktional:

Die zugehörigen LAGRANGEgleichungen lauten:
Es handelt sich um N Differentialgleichungen 2.Ordnung. Diese können in 2N Differentialgleichungen 1.Ordnung umgeschrieben werden. Wir definieren dazu die verallgemeinerten Impulse:
Diese Gleichung sei im folgenden auflösbar nach ![]() (t). Damit können wir
schreiben:
(t). Damit können wir
schreiben:
Aus Gleichung (1), (2) und (3) ergibt sich dann:
Dies sind 2N Gleichungen 1.Ordnung für p und q. Hierbei gelten folgende Aussagen:
Wir setzen Gleichung (3) in (4) ein:
Was heißt, daß p(t) = Lv(t,q(t),![]() (t)) nach
(t)) nach ![]() auflösbar ist? Im Falle N = 3
gilt:
auflösbar ist? Im Falle N = 3
gilt:
Damit diese Gleichungen nach ![]() 1,
1, ![]() 2,
2, ![]() 3 auflösbar sind, muß detLvjvk
3 auflösbar sind, muß detLvjvk![]() 0 gelten für
j, k = 1, 2, 3.
0 gelten für
j, k = 1, 2, 3.
Falls T(u,v) = ![]() v
v![]() A(u)v und L(t,u,v) = v
A(u)v und L(t,u,v) = v![]() A(u)v - U(t,u) ist, gilt L
v = Av. Das
Gleichungssystem lautet dann p(t) = A(q(t))
A(u)v - U(t,u) ist, gilt L
v = Av. Das
Gleichungssystem lautet dann p(t) = A(q(t))![]() (t). Auflösbarkeit nach
(t). Auflösbarkeit nach ![]() (t) bedeutet
gerade Invertierbarkeit von A(u) (beispielsweise wenn T(u,v) = v positiv definit
ist).
(t) bedeutet
gerade Invertierbarkeit von A(u) (beispielsweise wenn T(u,v) = v positiv definit
ist).
Betrachten wir folgenden Energieausdruck:
Es gilt daher für die HAMILTONfunktion H:
Wir bezeichnen im folgenden q(t) mit u und p(t) mit w und differenzieren formal nach w:
Damit folgt für die erste HAMILTON-Gleichung:
Nun zur Herleitung der zweiten HAMILTON-Gleichung. Dazu differenzieren wir formal nach u:
Außerdem gilt:
Es gilt ![]() (t,q(t),p(t))
(t,q(t),p(t)) ![]()
![]() N; es handelt sich also um einen N-dimensionalen Vektor.
Was heißt
N; es handelt sich also um einen N-dimensionalen Vektor.
Was heißt ![]() w(t,q(t),p(t)) . p(t)? Dazu führen wir die Berechnung explizit
durch:
w(t,q(t),p(t)) . p(t)? Dazu führen wir die Berechnung explizit
durch:
![]() w(t,q(t),p(t)) . p(t) ist ein Vektor. (Es handelt sich gewissermaßen sogar um ein
Tensorprodukt.)
w(t,q(t),p(t)) . p(t) ist ein Vektor. (Es handelt sich gewissermaßen sogar um ein
Tensorprodukt.)
Wir betrachten die LAGRANGEfunktion:
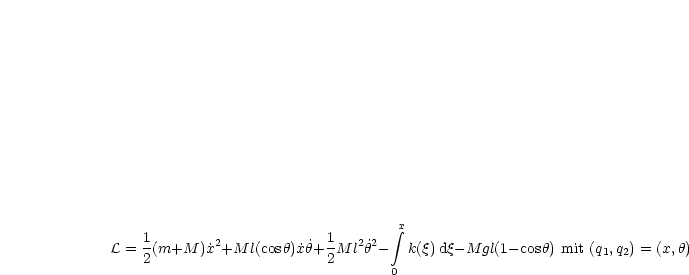
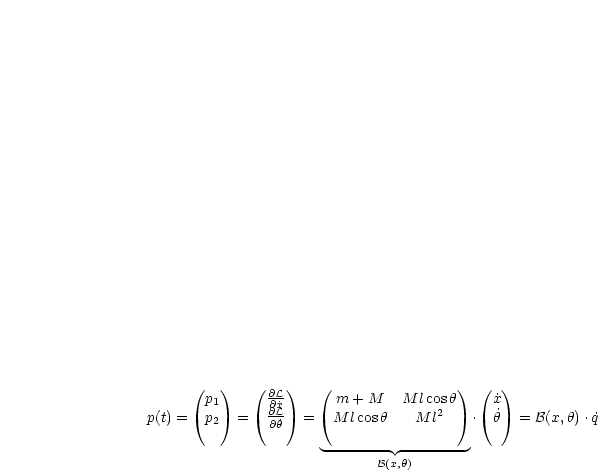
Hieraus ergibt sich dann durch Auflösen nach ![]() (t):
(t):

Hierbei gilt:

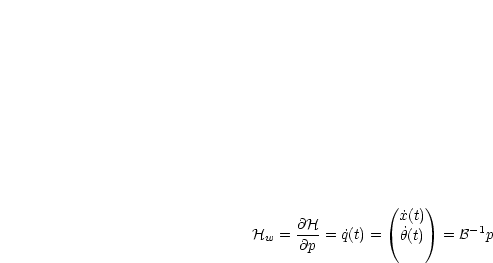

Mit p(t) = Lv = (t,q(t),![]() (t)) ergibt sich:
(t)) ergibt sich:
Man spricht hier auch von der Normalform der Gleichungen.