1.8 Hamilton-Prinzip

1.8 HAMILTON-Prinzip

Wir stellen uns vor, daß der Zustand eines physikalischen Systems zur Zeit t durch einen Vektor (t) = mit t [t₀,t₁] festgelegt wird. L = L(t,q₁,...,q_n,p₁,...,p_n) sei die zugehörige LAGRANGE-Funktion. Der im Zeitintervall [t₀,t₁] bei bekannten Zuständen ₀ = (t₀) (Anfang) und ₁ = (t₁) (Ende) ablaufende Vorgang wird durch die Kurve = _m(t) beschrieben, die das Wirkungsintegral

integral t1 S(f) = L(t,f1(t),...,fn(t);f'1(t),...,f'n(t))dt t0

minimal (oder wenigstens stationär) macht und _m(t₀) = ₀ und _m(t₁) = ₁ erfüllt.

Zusammenfassung aus den vorhergehenden Beispielen:

Jeweils liegt eine Vorschrift vor, die Funktionen aus einer Funktionenmenge () eindeutig eine reelle Zahl zuordnet. Wir haben also folgende Vorschrift:

F : D '--> R

F nennt man nun Funktional („Funktionfunktion“). Gesucht sind Elemente y aus , für die F(y) extremal wird. In HMII hatten wir folgendes Problem:

m f : M (_ R '--> R

y = f(x ,...,x ) 1 m

Hier hatten wir endlich viele Unbekannte. Nun betrachten wir aber y = F() und hier handelt es sich um „unendlich viele Unbekannte“zur Festlegung einer Funktion.

Gesucht ist eine C²-Funktion, welche die kürzeste Verbindung zweier Punkte einer Geraden beschreibt, die in den Punkten A und B senkrecht auf der Geraden steht.

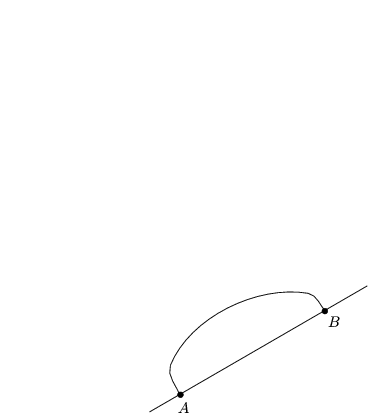
Man wird feststellen, daß dieses Problem keine Lösung besitzt.
Voraussetzung, daß eine Lösung existiert, muß rückwirkend bestätigt werden.
„Die größte ganze Zahl G ist gleich 1.“
Da 1 , folgt G > 1. Falls G > 1 folgt, G² > G. Dies geht nicht, da mit G aus G² und G schon die größte ganze Zahl ist. Daraus folgt dann G = 1. Wir haben wir vorausgesetzt, daß es eine größte ganze Zahl gibt, weshalb wir auf diesen Unsinn kommen!
Minimum auf : $integral +1 F(y) = x4y'2dx -1$

${ } D = y (- C^1[- 1,+1]/y(-1) = -1,y(1) = 1$

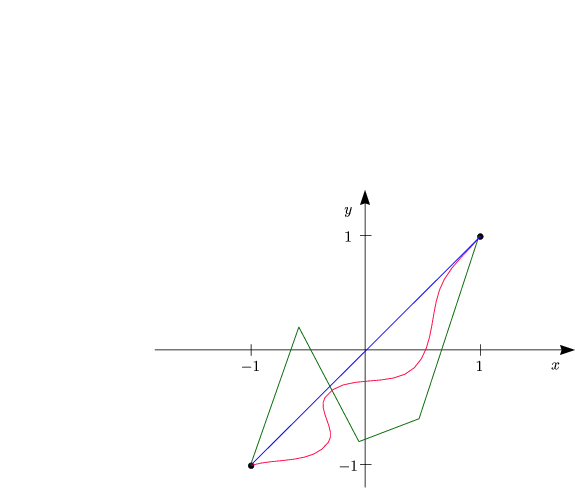
Da F(y) > 0, ist die Frage nach einem Minimum keinesfalls sinnlos! Aus y' = 0 folgt y(x) = const. . Wenn das Problem also durch y_m lösbar ist, muß F(y_m) > 0 sein. Es sei y_m eine Lösung, also gelte F(y_m) = a > 0.

$-1 f¨ur - 1 < x < - e { 1 ye(x) = ex f¨ur - e < x < e 1 f¨ur e < x < 1$
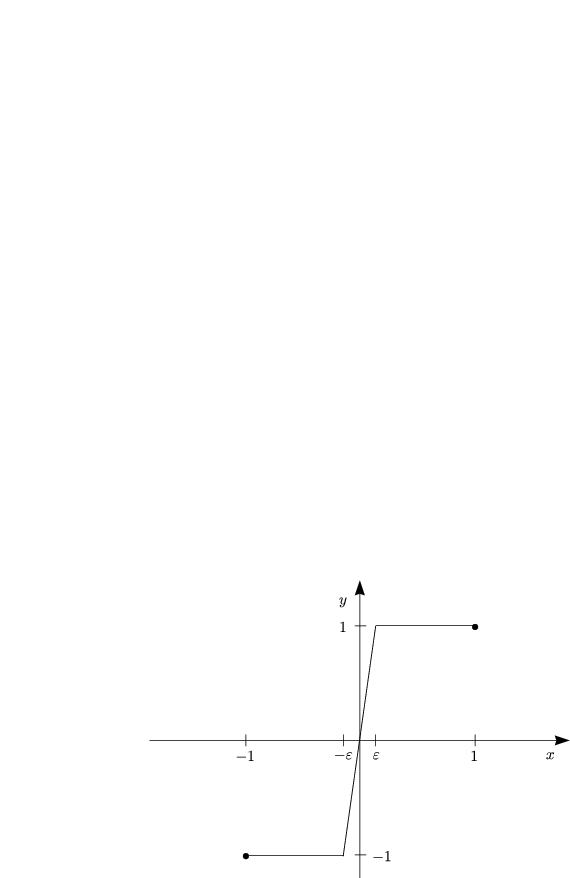
Durch Nachrechnen erhält man:
$0 < F(y ) = 2e3(< a) e 5$
Also erhalten wir:
$V~ --- e < 3 5a 2$
Das geht für jedes Zahl a > 0. Unser Problem hat folglich keine Lösung!

Bemerkungen:

Es wird fast ausschließlich ¹. Es handelt sich um einen Vektorraum. ist jedoch im allgemeinen kein Vektorraum. Als Beispiel betrachten wir: ${ } ( ) D = y (- C1[a,b]| y(a) = a1,y(b) = b1 a21 + b21 /= 0$
Dies ist kein Vektorraum, denn aus y₁, y₂ folgt y₁(a) + y₂(a) = 2a₁. ist sehr oft eine konvexe Menge.

D heißt konvex, falls aus y₁, y₂ M folgt, daß t₁ + (1 - t)₂ M für alle t [0,1]. Eine konvexe Funktion y = f(x) ist beispielsweise:

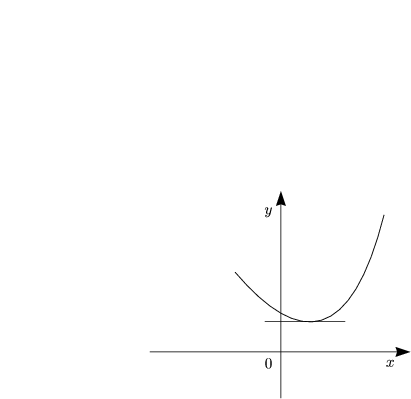
Für konvexe Funktionen gilt nach unserer Definition f'' > 0. (Die Ableitung liegt immer außerhalb der Menge.)
$a != ty (a)+ (1- t)y (a) = ta + (1- t)a = a 1 1 2 1 1 1$

$! b1= ty1(b)+ (1- t)y2(b) = b1$
Die Voraussetzungen zur Konvexität sind also erfüllt.

[prev] [prev-tail] [front] [up]