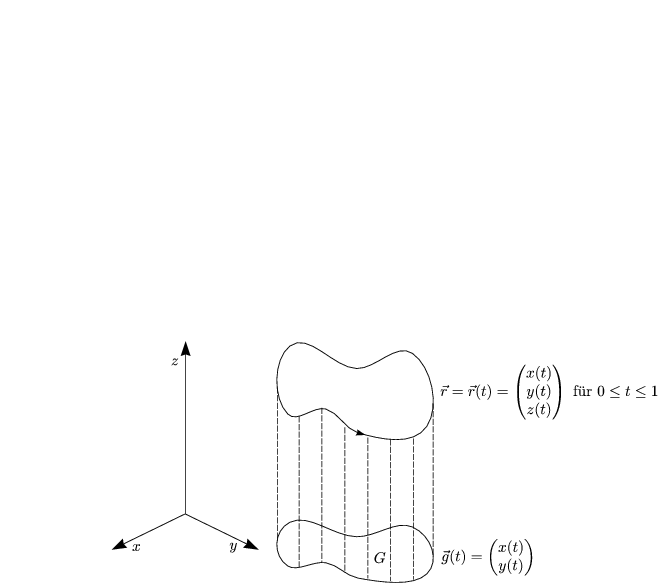
Gesucht ist die Fläche F: z = f(x,y) mit (x,y) 
G und z(t) = f(x(t),y(t)) für
0 < t < 1 derart, daß der Inhalt von F = A(f) = 
G
d(x,y) minimal
wird.
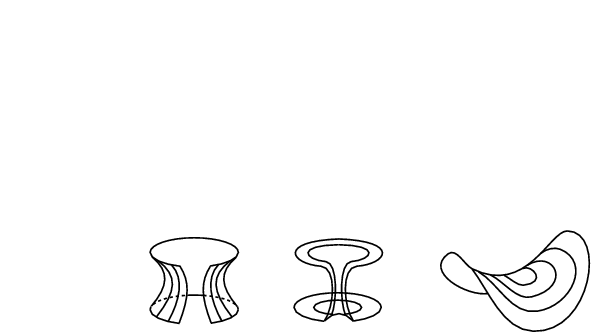
Gesucht ist Kurve y = y(x) durch A und B derart, daß der durch Rotation der Kurve um die x-Achse entstehende Körper minimale Oberfläche hat.
