Kapitel 6
Geladenes Teilchen im Magnetfeld

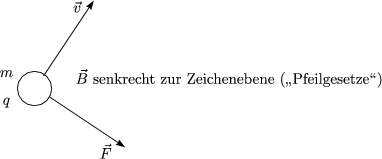
ist homogen, zeitlich konstant und parallel zur z-Achse.

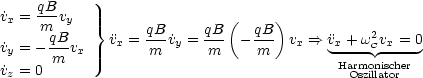
Es ist ein Glücksfall, da x, y, z nicht explizit in diesen Differentialgleichungen vorkommen. Damit ergibt sich die Zyklotronfrequenz:

v₀ und sind die beiden unabhängigen Konstanten, die wir benötigen.

Die Ortskurven folgen durch Integration:

x₀, y₀, z₀ sind die drei weiteren Konstanten. Das Teilchen beschreibt eine Kreisbahn in der x-y-Ebene mit dem Mittelpunkt (x₀,y₀) und dem Radius .

Erhaltungsgrößen:

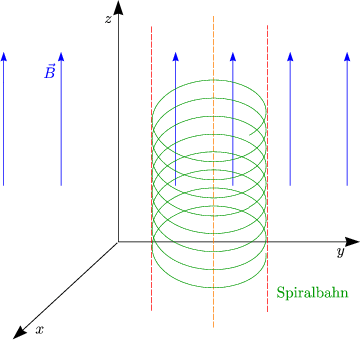
Hier gibt es wiederum 2S - 1 = 5 Integrale der Bewegung.

• Drehimpuls: = ×

  Aber wenn man die z-Achse auf Spiralachse legt (x₀ = 0,y₀ = 0), dann ist der Drehimpuls erhalten.

• Energie

• Geschwindigkeitskomponente in z-Richtung

  v_z ist auch ein Integral der Bewegung.

Bewegungsintegrale müssen zeitunabhängig sein für alle möglichen Bahnen (vergleiche Seite 48) und nicht nur für spezielle Bahnen, deren Spiralachse auf der z-Achse liegt! Außerdem ist, selbst unter dieser Bedingung, nur die z-Komponente des Drehimpulses (um den Ursprung) erhalten (es sei denn v_z = 0). Vergleiche dazu außerdem Skript Theorie B auf Seite 37.