5 Erhaltungsgrößen

Kapitel 5
Erhaltungsgrößen

Man nennt eine physikalische Größe G = G(x,v,t) eine Erhaltungsgröße, falls G = G(x(t),v(t),t) = const. längs der Bahnkurve. Wieviele unabhängige Erhaltungsgrößen (Bewegungsintegrale) gibt es überhaupt?

} x(t) = x(t,C1,C2,...,C2S) v(t) = ˙x((t,C1,C2,...,C2S) 2SGleichungen

S=Raumdimension × Zahl der Teilchen=Zahl der unabhängigen Koordinaten

Man löst nach C₁, C₂, ..., C_2S auf. C_j ist eine Funktion von t, x₁, ..., x_S, v₁, ..., v_S. Auf der Bahnkurve x_j = x_j(t), v_j = v_j(t) ist der Wert dieser Funktion konstant. Erhaltungsgrößen können eine solche Funktion selbst sein oder oder aus Kombinationen dieser Funktionen zusammengesetzt sein.

Bemerkung:

Wenn

unabhängig von t ist, dann kommen t, t₀ (Zeitnullpunkt) nur in der Form t - t₀ vor.

( ) xj(t) = xj t -t0,C1,C2,...,C2S- 2S-1 IdB

Es sind somit nur 2S - 1 Integrale der Bewegung, die nicht explizit von t abhängen.

Eindimensionaler Oszillator (ungedämpt):

mx¨ = -Dx

S = 1, Bewegungsintegrale: 2S = 2,2S -1 = 1

Es gibt somit ein Bewegungsintegral, das nicht explizit von t abhängt.

x = x0cos(wt- f)

v = -x0w sin(wt- f)

E(x,v) = 1mv2 + 1 Dx2 ~ x20 2 2

E(x,v) ist konstant, da x₀ konstant ist!.

x- -1 v = -w cot(wt - f)

( xw ) wt -f = arccot --v-

Beispiele:

(Vergleiche hierzu auch Seite 52!)

Impuls eines Teilchens $dp-= F(r,v,t) = 0, wenn p erhalten. dt$
N-Teilchen $sum N dpj = Fjk + F ejxt dt k=1$
Die Kraft setzt sich also zusammen aus F_jk, nämlich der Kräfte auf das Teilchen j, die von allen anderen Teilchen herrühren und der äußeren Kräfte.
Gesamtimpuls $N sum Pges = pj j=1$

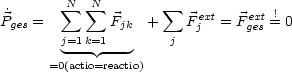
$N N ˙P = sum sum F + sum F ext= F ext=!0 ges j=1k=1 jk j j ges --- --- =0(actio=reactio)$
Genau dann ist _ges erhalten.

G(x,y) ist Funktion von Ort und Geschwindigkeit aller Teilchen. Sie ist erhalten, wenn G = 0 ist. Man versucht, Aussagen für ALLE möglichen Bahnen zu liefern.

Bewegungsgleichungen: $dp- dt = F$
Impuls: $dp(t) -dt--= F : Integral der Bewegung, wenn F = 0$
Energie: $dv(t)- m dt = F$

$m .v dv= vF dt$
Es gilt:
$( ) d- a .b = ˙a.b + a.˙b dt$

$( ) d- m-v2 = 0, wenn v _L F dt -2 -- Ekin$

Lorentzkraft:

F = q.v × B(r,t) = Ladung.Geschwindigkeit× Magnetfeld

E_kin = v² Dies ist ein Integral der Bewegung:
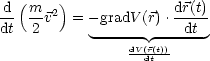
= -gradV $d (m ) dr(t) -- --v2 = - gradV (r).----- dt 2 ------ ---dt- dV(dr(tt))$

$Eindimensional: dV-(x).dx-= dV(x(t))- dx dt dt$

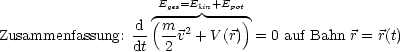
$Eges=Ekin+Epot d-(m- 2 ) Zusammenfassung: dt 2 v + V (r) = 0 auf Bahn r = r(t)$
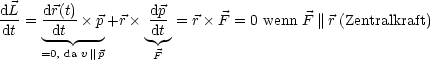
Drehimpuls = × geht IMMER. $dL- dr(t)- dp- dt = -dt ×-p +r× dt = r × F = 0 wenn F ||r (Zentralkraft) =0, da v||p F$
In diesem Fall ist ein Integral der Bewegung.

Freies Teilchen:

Kepler-Problem

( ) F = - GM-m- r ,V = -G M-m- r2 r r

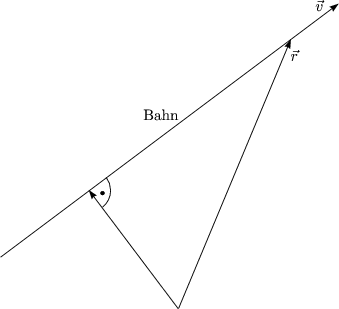
Es gibt 2S - 1 = 5 unabhängige Erhaltungsgrößen.

= × , da Zentralkraft
3 Integrale der Bewegung
E = ² + V ()
1 Integral der Bewegung
Eine eindimensionale Erhaltungsgröße: Lenz-Runge-Vektor $( ) /\ = v× L - GM m r r$

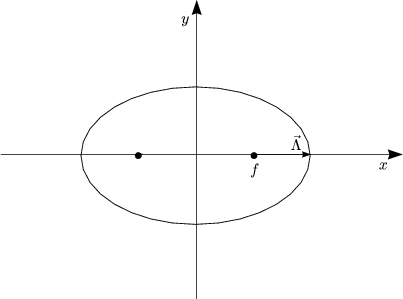
Der Lenz-Vektor zeigt zum Perihel. Die Abweichung von ~ führt zur Drehung des Perihels. Die Bahn ist nicht mehr geschlossen. Für den Planeten Merkur gilt beispielsweise:

Abweichung ~ 600

Die allgemeine Relativitätstheorie hat einen Beitrag von 42 Bogensekunden.

[next] [prev] [prev-tail] [front] [up]

Kapitel 5Erhaltungsgrößen