4.2 Sonne im Brennpunkt

[next] [prev] [prev-tail] [tail] [up]

4.2 Sonne im Brennpunkt

a = 4 } V~ ----- V~ - b = 3 f = 16 - 9 = 7

Polarkoordinaten:

x = rcosf

y = r sinf

r(f) = ----p---- 1+ ecosf

0 < e < 1 Ellipse

Parabel: e = 1

Hyperbel: e > 1

4.2.1 Bewegungsgleichung

( ) d2r(t) m-.MSonne- r m dt2 = F (r) = -G r2 r

Die Bahn liegt in einer Ebene. Für den Drehimpuls gilt: = (t) × (t)

dL dt-= 0

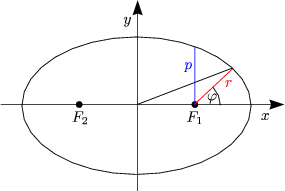
ist nach Richtung und Betrag fest. steht senkrecht auf der Bahnkurve. Für eine Kreisbahn gilt:

L = r.m .v

v = r.w

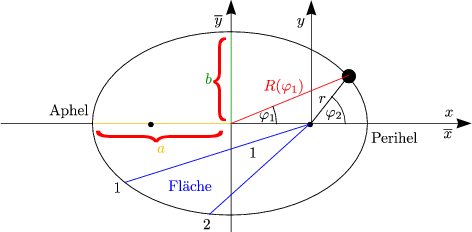
Planten und periodische Kometen beschreiben Ellipsen:

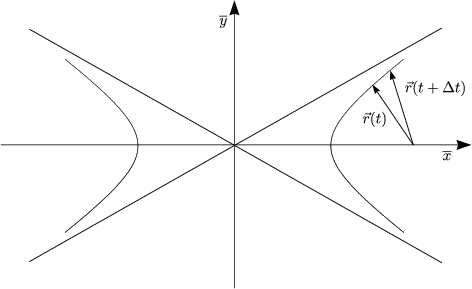
Einmalige Kometen beschreiben Hyperbeln:

Zusammenfassung:

Mittelpunkt $-- -- x2 - y2= 1 a2 b2$

$f = V~ a2---b2$
Parameterdarstellung $x = acosht$

$y = bsinh t$
Brennpunktlage $r = ---p----- 1+ ecosf$
Die Exzentrizität ist definiert durch:
$|-----| | f-| -e =-a-$
Hierbei gilt nun für die verschiedenen Kegelschnitte:
- Ellipse: < 1
- Kreis: = 1
- Hyperbel: > 1

Wiederholung: Kepler-Gesetze

Bahn in einer Ebene, Sonne im Brennpunkt der Ellipsen/Hyperbeln (=const.)
Flächensatz (Zeitfall) (||)
T² ~ a³ (unabhängig von b)

Bewegungsgleichung:

d2r(t) m .M ( r ) m ---2- = -G ---2-o. -- nicht linear in r! dt |r| |r|

Die Bahn liegt in einer Ebene. Der Drehimpuls ist somit erhalten:

L = r × p = r(t) × p(t)

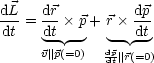
dL dr dp --- = --× p + r× --- dt dt -- --dt- v|| p(=0) dpdt||r(=0)

4.2.2 Flächensatz

Hier benötigen wir unter anderem v = r ^.

. Dies wollen wir zuerst zeigen:

( ( )) ( ) df d arctan yx 1 d yx 1 y˙x - y˙x 1 [(x) (x˙)] 1 w = dt-= -----dt-----= ---(y)2-.-dt--= 1-+-y2.---x2-- = x2 +-y2-. y × y˙ = r2(r ×v) = 1+ x x2 = 1-.(r.v.sina) = 1-.(r.v _L ) = v _L r2 r2 r

(4.1)

Damit gilt nun:

1 DA = 2 (r.Df) .r+ Korrektur in (Df)2

( ) DA-= 1r2 Df- D--t-'-->-0--> dA(t)= 1 r2(t).df(t) Dt 2 Dt dt 2 dt

Der Flächensatz folgt auch einfacher direkt aus der Drehimpulserhaltung:

1 dA = 2rds _L

dA-= r .v _L = 1(r × v) = const. dt 2 2

[next] [prev] [prev-tail] [front] [up]