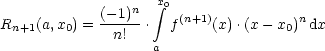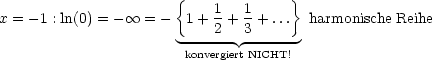2.5 Taylor-Reihe

[next] [prev] [prev-tail] [tail] [up]

2.5 Taylor-Reihe

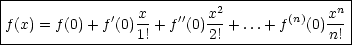
|-------------------------------------------| | ' x- '' x2 (n) xn-| -f(x) =-f(0)+-f-(0)1! +-f-(0)2!-+-...+-f-(0)n!-

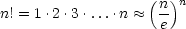
( )n n! = 1.2.3 .....n ~~ n- e

Beispiel:

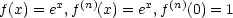
f (x) = ex,f(n)(x) = ex,f(n)(0) = 1

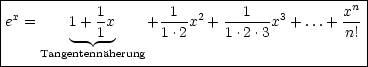
|-------------------------------------------n-| |ex = 1+ 1x +-1--x2 +---1--x3 + ...+ x-| | --1-- 1 .2 1 .2.3 n! | -----Tangentenn¨aherung-----------------------------

Die Reihe kovergiert (für |x| < 1) besser als geometrische Reihe.

2.5.1 Naive Kovergenzbetrachtung

Vergleiche mit geometrischer Reihe: 1 + q + q² + ... + qⁿ + ... mit |q| < 1

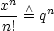
n x-- /\ = qn n!

|--|--|--|-|--|-|---|--------|-|-|--| |x-|--|x-|-|x-|-|x--|x-------|-|-|x-| -1--.--2--.-3----[x]-([x]+-1)------n-

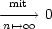
--m-i-t--> 0 n'-->o o

Quotient zweier aufeinanderfolgender Glieder:

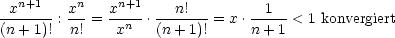
-xn+1-- xn- xn+1- --n!--- --1-- (n + 1)! :n! = xn .(n+ 1)! = x .n+ 1 < 1 konvergiert

Betrachten wir die Taylor-Reihe einer Funktion f(x):

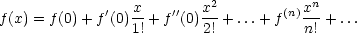
2 n f(x) = f(0)+ f'(0)x-+ f''(0)x +...+ f(n)x-+ ... 1! 2! n!

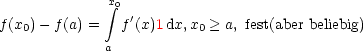
integral x0 f(x0)- f(a) = f '(x)1dx,x0 > a, fest(aber beliebig) a

Wir führen eine partielle Integration durch:

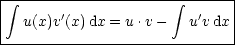
|-----------------------------| | integral ' integral ' | | u(x)v(x)dx = u .v- u vdx | ------------------------------

[u(x) .v(x)]'= uv'+ u'v

Außerdem gilt ja:

|-------------| | integral ' | | [uv] dx = uv| --------------

u(x) = f'(x)

v'(x) := 1 ==> v(x) = x + const. (const. = -x0)

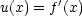
x x integral 0 ' ' x=x integral 0 '' f(x0) = f(a)+ f (x) .1 dx = f (a)+ [f (x)(x- x0)]x=a0 - f (x).(x- x0)dx = a a integral x0 = f(a)+ f'(x0)(x0 - x0)- f'(a)(a- x0)- f''(x).(x -x0)dx = a x integral 0 = f(a)+ f'(a)(x0- a)- f''(x)(x- x0)dx a

(2.2)

Wir integrieren nochmals partiell:

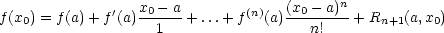
' x0--a- (n) (x0--a)n f(x0) = f(a)+ f (a) 1 +...+ f (a) n! + Rn+1(a,x0)

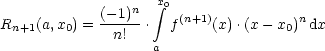
(-1)n x integral 0 Rn+1(a,x0) =----- . f(n+1)(x).(x- x0)ndx n! a

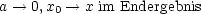
a --> 0,x0 --> x im Endergebnis

R_n+1(a,a) = 0 x₀ = a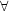n
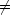R_n+1(a,x₀)0 mit n (x₀a)
Für |x₀ - a| < r hat die Reihe hat den „Konvergenzradius“ r.
R_n+1 / 0 für n für alle x₀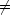a

Beispiel:

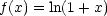
f(x) = ln(1+ x)

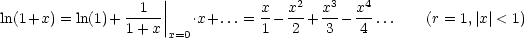
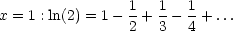
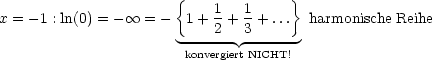
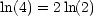
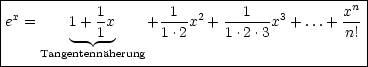
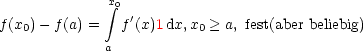
| --1--|| x- x2 x3 x4 ln(1+x) = ln(1)+ 1+ x |x=0.x+...= 1- 2 + 3 - 4 ... (r = 1,| x|< 1)

1 1 1 x = 1 : ln(2) = 1- 2 + 3 - 4 + ...

{ } x = -1 : ln(0) = - oo = - 1 + 1+ 1+ ... harmonische Reihe ----2-- 3------ konvergiert NICHT!

ln(4) = 2ln(2)

( ) ( ) 5 5 ln(5) = ln(2 + 3) = ln 4 .4 = 2ln(2) + ln 4

[next] [prev] [prev-tail] [front] [up]