Größen haben immer einen Wert (reelle Zahl mit unendlich vielen Dezimalen!), eventuell kennt man den nicht genau. Die Streuung des Werts einer Größe ist defniert durch:
<x> sei dabei der Mittelwert einer Meßreihe. In der klassischen Physik ist ![]() G eine
Folge von Fällen einer Größe G. Die Wirklichkeit erkennen wir dann, wenn wir Atom-
und Quantenphysik betreiben. Es gibt Variablen wie beispielsweise px, x, wofür es
keine Zustande gibt, für die sowohl
G eine
Folge von Fällen einer Größe G. Die Wirklichkeit erkennen wir dann, wenn wir Atom-
und Quantenphysik betreiben. Es gibt Variablen wie beispielsweise px, x, wofür es
keine Zustande gibt, für die sowohl ![]() x als auch
x als auch ![]() px beide („simultan“) = 0
sind.
px beide („simultan“) = 0
sind.
Dies ist keine physikalische Größe im obigen Sinn.
![]() . d
. d![]() ist das Skalarprodukt der Vektoren
ist das Skalarprodukt der Vektoren ![]() und d
und d![]() , wobei d
, wobei d![]() =
= ![]() . dt
das sogenannte Differential ist.
. dt
das sogenannte Differential ist.
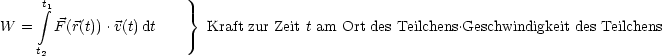
W ist Prozessgröße (Folge von Zuständen). x ist eine unabhängige und y eine abhängige Variable.
