Ortsvektor (Anfang festgelegt)
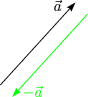
![]() =
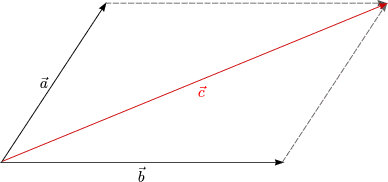
= ![]() +
+ ![]() =
= ![]() +
+ ![]() (kommutativ)
(kommutativ)
Ortsvektor (Anfang festgelegt)

![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() (kommutativ)
(kommutativ)

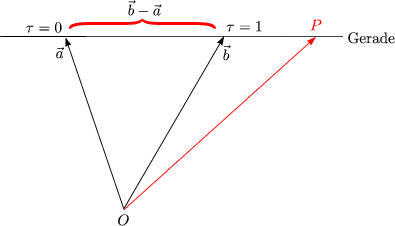

![]() ,
, ![]() sind die sogenannten Schar-Paramter.
sind die sogenannten Schar-Paramter.
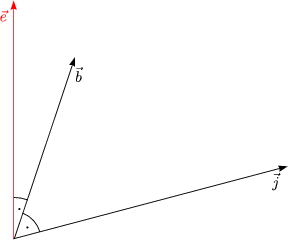
|![]() . (
. (![]() ×
×![]() )| ist das Volumen des Spats, welcher von den drei Vektoren
)| ist das Volumen des Spats, welcher von den drei Vektoren ![]() ,
, ![]() und
und ![]() aufgespannt wird.
aufgespannt wird.

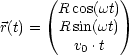
Ganghöhe=const.