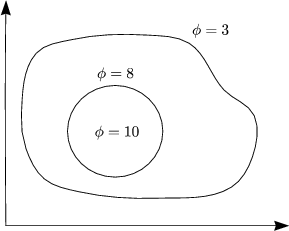

Einem Punkt ![]() = (x,y,z) wird eine Zahl
= (x,y,z) wird eine Zahl ![]() =
= ![]() (
(![]() ) zugeordnet. Die Linien, auf denen
) zugeordnet. Die Linien, auf denen
![]() konstant ist, nennt man Iso-
konstant ist, nennt man Iso-![]() -Linien (Äquipotentialflächen).
-Linien (Äquipotentialflächen).
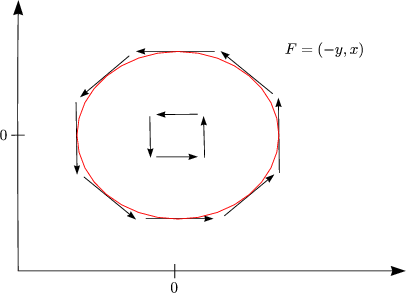
Jedem Punkt ![]() = (x,y,z) wird ein Vektor
= (x,y,z) wird ein Vektor ![]() =
= ![]() (
(![]() ) zugeordnet.
) zugeordnet.
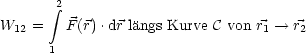
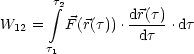
Die Kurve wird beschrieben durch ![]() =
= ![]() (
(![]() ). Radial (C2):
). Radial (C2):
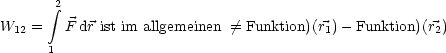
Die Arbeit ist auch mit geeignet gewählter Funktion f abhängig vom Weg, der die
Punkte ![]() und
und ![]() miteinander verbindet. Sie ist eine Prozess-Größe im Gegensatz zur
Energie, welche eine Zustandsgröße darstellt. Wir stellen uns deshalb nun die
Frage:
miteinander verbindet. Sie ist eine Prozess-Größe im Gegensatz zur
Energie, welche eine Zustandsgröße darstellt. Wir stellen uns deshalb nun die
Frage:
Für welche Kraft-Felder ist W = ![]() 12
12![]() d
d![]() = -[
= -[![]() (
(![]() ) -
) - ![]() (
(![]() ] unabhängig vom Weg,
der
] unabhängig vom Weg,
der ![]() und
und ![]() verbindet?
verbindet?
![]() (
(![]() ) entspricht dabei der potentiellen Energie. In einer Dimension gibt es kein
Problem mit Wegabhängigkeit:
) entspricht dabei der potentiellen Energie. In einer Dimension gibt es kein
Problem mit Wegabhängigkeit:
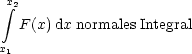
Aber in zwei Dimensionen ist ![]()
![]() (x(
(x(![]() ),y(
),y(![]() )) .
)) .![]() d
d![]() verschiedener
Integrand für verschiedene Wege.
verschiedener
Integrand für verschiedene Wege.