2.9 Mathematischer Einschub: Vollstndiges Differential, Gradient

[next] [prev] [prev-tail] [tail] [up]

2.9 Mathematischer Einschub: Vollständiges Differential, Gradient

f(x,y) sei eine Funktion von 2 (und mehr) unabhängigen Variablen. Dabei gilt nun:

Partielle Ableitungen: ( mit y = const.)
Operator-Schreibweise: =
_Diff.Op.f(x,y)

f(x,y) mit x = x(t),y = y(t)

Die Funktion f(x,y) liegt somit auf der Kurve C.

P(t) := f (x(t),y(t))

P˙(t) = dP(t) dt

Beispiel: f(x,y) = xy

P(t) = x(t)y(t)

Wir leiten (t) nach der Variable t ab:

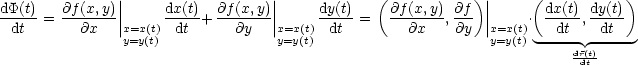
| | ( )| ( ) dP(t) = @f-(x,y)|| dx(t)+ @f(x,y)|| dy(t)= @f-(x,y), @f || . dx(t), dy(t) dt @x |x=x(t) dt @y |x=x(t) dt @x @y |x=x(t) --dt- -dt-- y=y(t) y=y(t) y=y(t) dr(t) dt

2.9.1 Der Gradient

Der Gradient ist ein Vektor der folgendermaßen definiert ist:

(@f(x,y,z) @f(x,y,z) @f(x,y,z)) gradf := ---@x----,---@y----,---@z----

Der Gradient hat die Eigenschaft, daß er senkrecht auf den Äquipotentialflächen steht.

In 3 Dimensionen: Äquipotentialflächen: (x,y,z) = const.
In 2 Dimensionen: Äquipotentiallinien: (x,y) = const.

Linie auf der A¨quipotentialfl¨ache

P(x,y,z) = const.

x = x(t),y = y(t),z = z(t)

-dP(x(t),y(t),z(t)) = 0 dt

dr(t) gradf(x,y,z)| xy==xy((t)t). dt = 0 z=z(t)

Beispiel:

Kreis: x2 + y2= R2 -- -- f(x,y)

grad f(x,y) = (2x,2y) = 2r

2.9.2 Totales (vollständiges) Differential

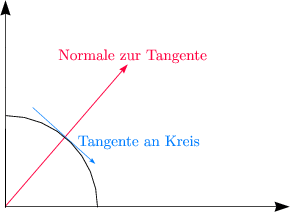
(Im Gegensatz zur partiellen Ableitung)

@f(x,y) @f(x,y) df := @x .dx + @y .dy

df = f'(x)dx

' Differential: dy = f (x)dx

' Tangente: y-- y0= f (x0).(x-- x0) dy dx

2 unabh¨angige Variable x,y

f(x,y,z) = const. Fl¨ache: z = z(x,y)

P0(x0,y0) /\ = Tangentialfla¨che

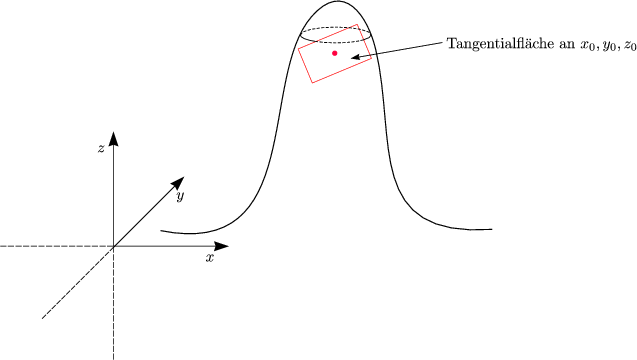
Tangentialfläche im Punkt (x₀,y₀,z₀)

- steht senkrecht zur Normalen der Ebene (Normale der Fläche im Punkt ). z = (x,y) erhält man durch Auflosen von f(x,y,z) =const.

F(x,y,z) = ~f(x,y)- z = 0

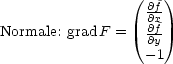
( ) @@fx~ Normale: gradF = @f~ @-y1

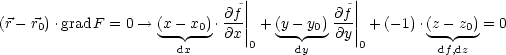
| | @ ~f|| @f~|| (r- r0).gradF = 0 --> (x- x0). @x|| + (y- y0)@y-|| + (- 1).(z- z0)= 0 dx 0 dy 0 df,dz

2.9.3 Vollständiges Differential einer Funktion f(x,y):

@f-(x,y) @x,y- df = @x dx+ @y dy

Auf C : r = r(t) : P(t) = f(r(t)) =_ f(x(t),y(t))

dP(t) @f(x,y)|| @f(x,y)|| dr(t) --dt- = --@x---||x=x(t).˙x(t)+ --@y---||x=x(t)y˙(t) = gradf(x,y)-dt- y=y(t) y=y(t)

Arbeit:

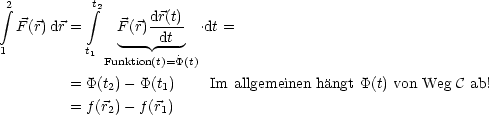integral 2 t integral 2 dr(t) F(r)dr = F-(r)-dt .dt = 1 t1 Funktion(t)= ˙P(t) = P(t2)- P(t1) Im allgemeinen h¨angt P(t) von Weg C ab! = f(r2)- f(r1)

(2.3)

Unter welchen Bedingungen an

(

) hängt W nicht von C ab?

Resultat:

F = gradf (r)

[ ] Physik: F = - gradV

(@f-(x,y) @f(x,y) ) Definition: gradf (x,y) = @x , @y ,...

Plausibilitätsbetrachtung:

F(r) = gradf siehe Einschub

integral W = P˙(t)dt = P(t2)- P(t1) = f(r2)- f(r1)

integral F dr = f(r2) - f(r1)

F (r) = grad f(r)

Wenn dies für alle Wege C (12) gilt, ist dann die hinreichende Forderung auch notwendig? Für benachbarte Punkte ₁, ₂ = ₁ + gilt:

integral integral F dr = Fx(x,y).dx+Fy(x, y).dy = Fx(x1,y1).Dx+Fy(x1, y1).Dy+ quadratische Anteile in Dx,Dy etc.

f(r2)-f(r1) /\ = df = @f(x,y).Dx+ @f(x,y)Dy+quadratische Anteile in Dx,Dy etc. @x @y

Gleichheit f¨ur ALLE Kurven 1 '--> 2, aber Dx,Dy unabha¨nig!

@f (x,y) @f (x,y) Fx(x,y) =------- Fy(x,y) =------- @x @y

Das heißt nun:

|-------------| | | F-=-gradf(x,y)-

Zusammenfassung:

Gegeben sei

(

). Wann gibt es ein f(

) mit

= gradf(

) [

= -gradV ]?

Eindimensionaler Fall: F(x) = - = - $x integral V(x) = - F (x) dx$
Zweidimensionaler Fall: F_x(x,y) = -,F_y(x,y) = -

V existiert nur dann, wenn:

@Fx(x,y)= @2V-(x,y) @y @x@y

@Fy(x,y) @2V-(x,y) @x = @y@x

|-------------------| |@Fx(x,y)= @Fy(x,y)| ----@y--------@x-----

Im dreidimensionalen Fall muß diese Bedingung für alle Paare (x,y), (y,z), (x,z) gelten. Dies schreibt man auch als:

( ) @@x- rot F(x,y,z) = o mit dem Vektoroperator rot = @@y × F. @@z-

Beispiele:

= $@Fx-= 0 =@Fy-= 0 @y @x$
(x,y) = $@Fx-= -1 /=@Fy-= +1 @y @x$

Außerdem gilt für eine Funktion F, die ein Potential besitzt, daß das Wegintegral (Ringintagral) d = 0 ist für alle geschlossenen Wege.

[next] [prev] [prev-tail] [front] [up]