2.13 Newton-Axiome (historisch)

[next] [prev] [prev-tail] [tail] [up]

2.13 Newton-Axiome (historisch)

= 0,(t) = ₀ ^. t + ₀ mit ₀,₀ =const.
0 : =
„actio=reactio“

2.13.1 Impulserhaltung

˙p1 = F1

˙p2 = F2

-d(p1 + p2) = F1 + F2=!0 dt

2.13.2 Energieerhaltung

Für ein Teilchen in einer Dimension gilt:

DE = v.Dp + (-F ).Dx + ...

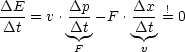
DE-= v .Dp- -F .Dx- != 0 Dt Dt Dt F v

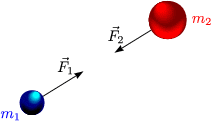
Sind die Änderungen unabhängig davon, wie sie vollzogen werden („wegunabhängig“)?

DE = E(r2,p2)- E(r1,p1)?

Eindimensional: $E(r,p) = p2-+ V(x), wenn F (x) = - @V(x) 2m @x$
Dreidimensional: $-p2 E(r,p) = 2m + V(r), F(r) = - gradV (r)$
N-Teilchensystem: $sum N p2 E(r1,p1,r2,p2,...) = -j--+ V(r1,r2,r3,...,rn) g=1 2mj$
Die x-Komponente der Kraft auf das j-te Teilchen F_xj berechnet sich nach -. Kräfte, die ein Potential haben, nennt man auch konservativ.

Für zwei Teilchen, die über eine Feder miteinander verbunden sind, gilt beispielsweise:

F1 = +D .(x2- x1 -a)

F2 = -D .(x2- x1 -a)

D V (x1,x2) =-2 (x2- x1 - a)2

[next] [prev] [prev-tail] [front] [up]