2.3 Differential-Schreibweise

} y = f(x) y /\ = Variable,f /\ = Funktion

y = y(x)

Die Ableitung wird dann als Grenzwert des Differentialquotienten definiert:

|------------f(x-+-Dx)---f(x-)-------Df--| f'(x0) = lim ---0-----------0-= lim --- | --------Dx'-->0--------Dx----------Dx'-->0-Dx--|

|------------| f '(x) = df-(x)| df nach dx ---------dx---

dx /= Dlixm'-->0Dx

df /= Dlixm'-->0Df

df, dx sind jedoch keine infinitesimal kleine Größen. Wir approximieren die Funktion durch eine Tangente:

y -y0 = f'(x0)(x- x0) - - -- -- dy dx(=Dx)

dy := f '(x ).dx 0

dy- ' dx = f(x0), x0 '--> x

|---------| |dy-= f'(x)| -dx--------

x, y sei laufender Punkt auf der Tangente.

Kettenregel: $' ' ' f(u(x)) '--> f (u(x)) = f (u).u (x)$
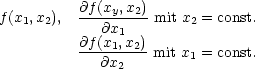
Mehrere Variable: $f(x1,x2), @f(xy,x2)mit x2 = const. @x1 @f(x1,x2)mit x1 = const. @x2$

$@f(...) @x partielle Ableitung$
Subsitutionsregel bei Integralen: $integral integral f (u(x)) dx = f(u).d(x(u)-.du -- -- -du-- u=oud(erx) -du1(x)- Umkxe=hxrf(uun)ktion dx$
Und x wird durch u eliminiert!