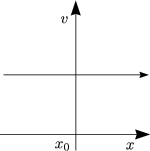
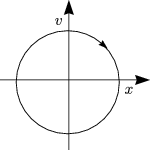
Ungedämpfter harmonischer Oszillator:
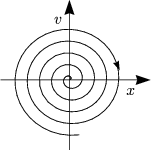
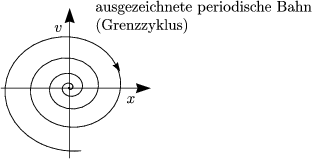
Wir haben ein eindimensionales mechanisches System, das aus einem Teilchen besteht:


Ungedämpfter harmonischer Oszillator:


Bahnen im Phasenraum schneiden sich NICHT! Wir betrachten ein allgemeines dynamisches System:
Bei f handelt es sich um einen n-dimensionalen Vektor. Im Gegensatz zur Mechanik darf n auch 1, 3, 5 sein. (Mechanik: n = 2 (x1 = x,x2 = v) etc., n = 4)
Hier haben wir nun zwei nicht linear gekoppelte Differentialgleichungen.
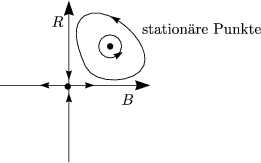
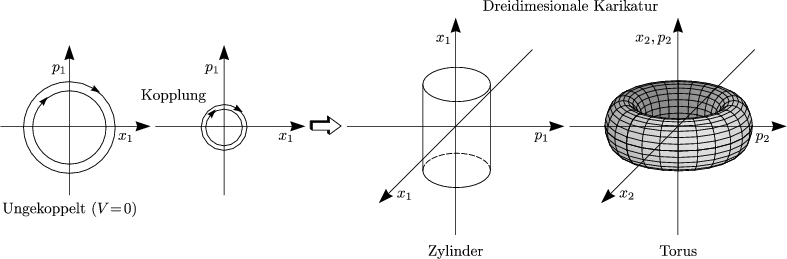
Poincaré-Schnitt______________ des 4d-Raumes mit x2 = 0 und p2 > 0