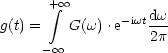5.7 Harmonischer Oszillator als Lineares System

[next] [prev] [prev-tail] [tail] [up]

5.7 Harmonischer Oszillator als Lineares System

f(t) (Input)

m = f(t) x(t) (Output)

Beispiel:

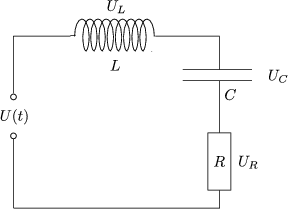
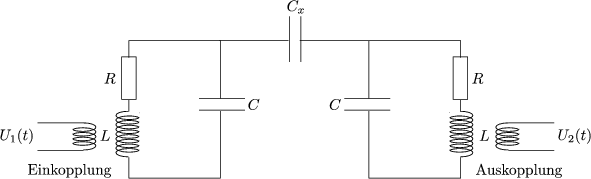
Unser Ziel ist es, x(t) für beliebige f(t) zu berechnen. Dazu gehen wir in zwei Schritten vor:

1.Schritt: Impulsförmige Kraft (x(t) 0 für f(t) 0, x(t)0 für t)

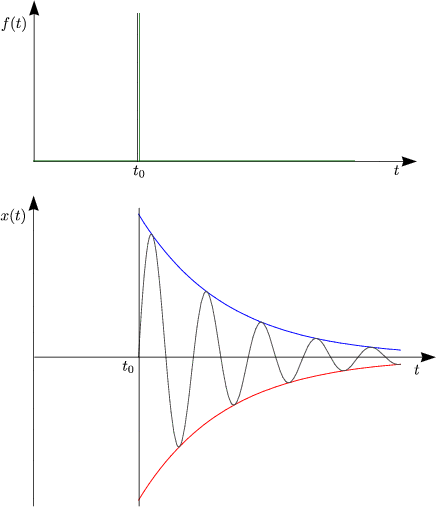
Für den Impulsübertrag p gilt f(t) = (p) ^. (t - t₀).
- t > t₀: $[ V~ ------- ] x(t) = A .e-g(t-t0) .sin w2- g2(t- t0)$
- t < t₀: $x(t) =_ 0$
Wie hängt A mit der Stärke des Kraftimpulses zusammen?
- Anfangsgeschwindigkeit: $------- V~ 2 2 v0 = A . w 0- g$
- Anfangsimpuls: $integral mv0 = f'(t')dt'$
Die Dirac-Funktion ist folgendermaßen definiert:
$d(t) /= 0 außerhalb t = 0$

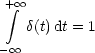
$+ oo integral d(t)dt = 1 - oo$

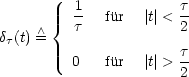
$1- f¨ur |t|< t- /\ { t 2 dt(t)= t 0 f¨ur |t|> 2-$

$[ ( )2] dt(t) =- V~ 1-exp - t- t p t$
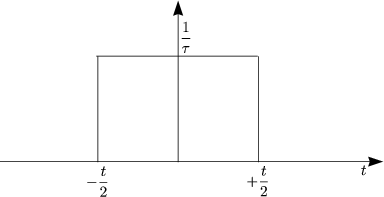
Der Grenzwert für 0 existiert im mathematischen Sinne nicht. Physikalisch gesehen ist eine sehr kleine Zeit. Nach dem Mittelwertsatz ergibt sich, wenn man , wie oben definiert, zugrunde legt:
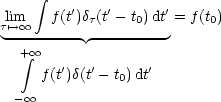
$integral lim f(t')dt(t'-t0)dt'= f(t0) t'-->o o ----- --------- + integral oo f(t')d(t'- t )dt' 0 - oo$

$Symmetrie: d(t) = d(- t)$
2.Schritt: $integral f(t) = f(t0)d(t- t0)dt0$

$Lo¨sung zu f(t0).d(t -t0) ist x(t) = f(t0).g(t,t0) Dp$

$|---------------------------------------------| | [ V~ -2---2- ] | |g(t,t) = 1-e-g(t-t0)sin---w V~ 0--g-(t--t0)- .h(t- t )| | 0 m w20- g2 0 | -----------------------------------------------$
Dies gilt auch für den aperiodischen Grenzfall und überdämpften Fall. Wir erhalten nun die Lösung für beliebige f(t), wobei wir die Linearität der Differentialgleichung ausnutzen:
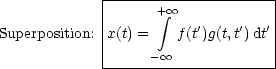
$|--------------------| | integral + oo | Superposition: x(t) = f(t')g(t,t')dt'| | - oo | ----------------------$
- Homogenität der Zeit: g(t,t') = g(t - t')
- Kausalität von x(t) und f(t): g(t,t') 0 für t' > t
- f(t) = f₀ cos(t) = Re $x(t) = Re [fe-iwt .G(w)] 0$
  
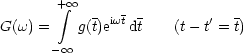
  $+ integral oo - iwt - ' - G(w) = g(t)e dt (t- t = t) - oo$
  Mit der Fouriertransformation folgt:
  $G(w) = G1(w) = +iG2(w) = A(w)eif(w)$
  
  $x(t) = f0A(w)cos(wt- f)$
  Die Fourier-Transformation ist (fast) selbstreziprok.
  $+ integral oo g(t) = G(w) .e-iwtdw- - oo 2p$

[next] [prev] [prev-tail] [front] [up]