
Wir arbeiten mit einer Koordinatentransformation, die den Ursprung O festhält
(Drehungen, Spiegelungen):

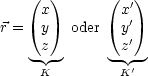
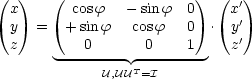
Die Werte von ![]() ,
, ![]() ' sind gleich, haben aber eventuell andere Form wie
beispielsweise:
' sind gleich, haben aber eventuell andere Form wie
beispielsweise:
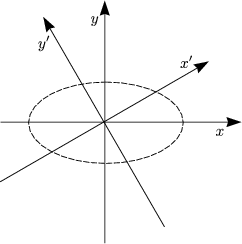
Invarianz, aber keine Forminvarianz
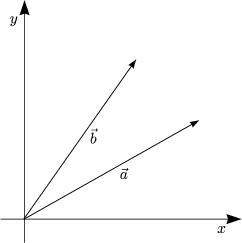
Die Komponenten von ![]() werden wie die Komponenten der Ortsvektoren
transformiert. Die Länge von Vektoren
werden wie die Komponenten der Ortsvektoren
transformiert. Die Länge von Vektoren ![]() ,
,![]() und der Winkel zwischen ihnen bleibt
invariant.
und der Winkel zwischen ihnen bleibt
invariant.
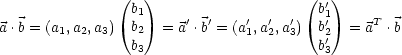
Dies wird folgendermaßen bewiesen:
Transformationsverhalten der Matrixelemente eines Tensors 2.Stufe
Diese sind aber leider etwas komplizierter in der Notation.