5.5 Bewegungsgleichungen des (freien) starren Krpers

5.5 Bewegungsgleichungen des (freien) starren Körpers

dP-= Fext=!0 (Kraft) dt

dL-= M ext=!0 (Drehung) dt

Körperfestes Koordinatensystem: Im Schwerpunkt
Raumfestes Koordinatensystem: Körper ruht

Bewegungsgleichung analog Massenpunkt m ^. = 0
Im raumfesten und körperfesten Koordinatensystem gilt:

L = I_O_

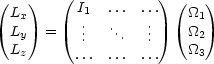
( ) ( ) ( ) Lx I1 ... ... _O_1 Ly = ... ... ... _O_2 Lz ... ... ... _O_3

Raumfestes Koordinatensystem (vertikal): $( ) dL (dI ) -dt = 0, aber dt- /= 0 rf rf$
Körperfestes Koordinatensystem: (nicht vertikal): $( ) dL- , aber dI-= 0 dt dt kf$

Es gilt:

( ) ( ) dA dA -dt = -dt + _O_× A rf kf

Und außerdem haben wir analog:

dR-= dR0-+ _O_× r dt dt

Wir betrachten nun L_x, wobei wir voraussetzen, daß der Trägheitstensor im körperfesten Koordinatensystem Diagonalgestalt hat:

( ) dLx- d- ! dt rf = dt (I1_O_x)kf +(_O_ × L)x- Komponente= 0

Wir nehmen nun an, daß das körperfeste Koordinatensystem ein Hauptachsensystem ist.

( ) I1 0 0 I = 0 I2 0 0 0 I3

Also folgt nun:

I1 ˙_O_x + _O_y Lz -_O_z Ly = 0 I3_O_z I2_O_y

Die Bewegungsgleichungen des freien starren Körpers lauten folglich:

I₁_x = (I₂ - I₃)_y_z
I₂_y = (I₃ - I₁)_z_x
I₃_z = (I₁ - I₂)_x_y

₁ , ₂ und ₃ sind die Komponenten der Winkelgeschwindigkeit bezüglich des körperfesten Koordinatensystems. Eigentlich noch Winkel ,, des körperfesten relativ zu raumfesten Koordinatensystem (Mehr im Fließbach)

Spezialfälle:

I₁ = I₂ = I₃ (Kugel, Würfel) $_O_ = const.$
I₁ = I₂I₃ $_O_3 = const.$

$[I2- I3 ] ˙_O_1 = --I---_O_3 ._O_2 ---1 ---- =const. (w2)$

$[ ] ˙ I3--I1 _O_2 = I2 _O_3 ._O_1 ---- ---- =const. (- w2)$
Daraus folgen nun die einfachen linearen Differentialgleichungen:
$_O_˙1 = wL ._O_2 } 2 2 ¨_O_1 = - wL_O_1 ==> _O_¨1 + wL_O_1 = 0 _O_˙2 = - wL ._O_1$
Die Lösungen sind somit:
$|---------------------| |_O_1(t) = a .cos(wLt+ f)| ----------------------$

$|---------------------| -_O_2(t) =---a.sin(wLt-+-f)$

$|--------| _O_3(t) =-b-$

Dies bezeichnet man als Larmor-Präzession, nach dem Physiker Larmor, der sich mit diesem Problem intensiv auseinandergesetzt hat.

[next] [prev] [prev-tail] [front] [up]