7.1 Dipolnherung

[next] [tail] [up]

7.1 Dipolnäherung

Fernzone:
Die eigentlich aufwendige Rechnung ist diejenige in der Fernzone:
$( ') ( ') k| x - x'|= k|x| 1 - xx-- = k|x| 1- nx- mit n =-x- |x |2 |x| |x| »1$
Nun folgt:
$1 1 ( xx') 1 ( x') |x---x'|-= |x| 1+ |x|2- = |x| 1+ n |x|-$
Der führende Term lautet:
$|-----------------------| | m0 eik|x| integral | A(x) = 4p--|x|- d3x'j(x')| -------------------------$
Wir formen dieses Integral um, wobei wir aufgrund der Übersichtlichkeit in folgender Nebenrechnung auf gestrichene Größen verzichten wollen:
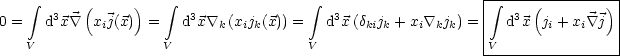
$|----------------| integral 3 ( ) integral 3 integral 3 | integral 3 ( ) | 0 = d x \~/ xij(x) = d x \~/ k (xijk(x)) = d x (dkijk + xi \~/ kjk) = | d x ji + xi \~/ j| V V V V-----------------$
Damit ergibt sich nun direkt, indem man den einen Term auf die linke Seite bringt:
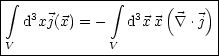
$|---------------------------| | integral 3 integral 3 ( ) | | d xj(x) = - d x x \~/ .j | -V------------V-------------$
Mit partieller Integration ergibt sich dies auch schneller:
$integral integral ( ) integral ( ) d3xj(x) = d3x j(x). \~/ x = - d3x x. \ ~/ .j(x)$
Eine eindimensionale Analogie ist:
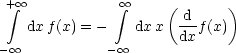
$+ integral oo integral oo ( ) dx f(x) = - dxx -d-f(x) - oo - oo dx$
Somit folgt:
$integral A(x) = m0eik|x|(- 1). d3x x( \~/ .j) 4p |x|$
Mittels der Kontinuitätsgleichung resultiert:
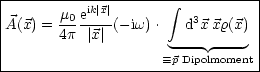
$|-------------------------------| | m0 eik|x| i ntegral | |A(x) = 4p-|x|-(-iw). d3xxr(x) | | ---- ---- | -------------------- =_ p-Dipolmoment$
fällt somit wie ab. Wir berechnen also und aus durch Ableiten:
$|----------| |------2------| -B-=- \~/ -×-A|und @tE-=-c- \~/ -×-B-$
Zur Erinnerung:
$' x-- \~/ f (| x|) = f (| x|)n mit n = |x|$
Somit folgt mit als konstanten Vektor:
$( ) \~/ × (f(|x| )c) = \~/ f (| x|) × c$
f(|) ist hier . Durch Ableiten ergibt sich:
$' ikeik|x| eik|x| f(|x| ) = |x| - x2$
Der erste Term ist führend für große ||.
$( ik|x| ) ik|x| B = \~/ × A = --im0w- \~/ × e-- p = -im0wik.e----(n× p) 4p |x| 4p |x|$

$|---------------------| | m0c eik|x| | |B = -4p k2-|x|-(n× p) | ----------------------$
folgt aus _t = c² $\~/$ ×. Analog zu eben folgt nun:
$( ) -iwE = ik n × B$

$|-------------| -E(x) =-cB-×-n-|$
Aus diesen Gleichungen kann man nun ablesen:
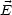
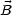
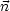
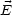- || = c||
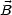Die radiale Abhängigkeit von E, B und A lautet damit folgendermaßen:
$|--------| |eik|x|--iwt-| | |x| | ---------$
Es handelt sich um eine Kugelwelle. Auf der Kugeloberfläche haben alle die gleiche Phase.
Nahzone (Quasi-Statischer Fall): $k|x|« 1,| x'|k « 1,| x'|« |x|$

$1 integral dx' ' f(x) = 4pe |x--x'|eik|x-x |r(x') 0$
Die Exponentialfunktion kann nun durch 1 angenähert werden. Damit folgt das Potential in der Elektrostatik:
$1 integral dx' f(x) = 4pe- |x---x'|r(x') 0$
Durch Entwicklung folgt wieder:
$integral ( ') f(x) =--1- 1-- dx' 1+ nx- r(x') 4pe0 |x| |x|$
Mit d'(') = 0 folgt:
$--1--1-- integral 3 ' ' ' f(x) = 4pe0|x|2 (n.p) mit p = d x x r(x )$

$- iwt E = (Dipolfeld wie in der Elektrostatik) .e$

[next] [front] [up]