7.2 M1- und E2-Strahlung

Wir behandeln im folgenden Dipol- und Quadrupol-Strahlung. Falls d³'(') = 0, dann behandeln wir den nächsten Term des Integranten bei der Taylor-Entwicklung.

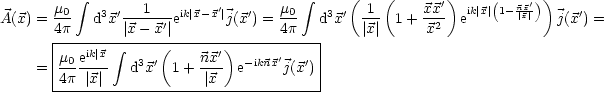integral integral ( ( ') ( ')) A(x) = m0 d3x'---1--eik|x-x'|j(x') = m0- d3x' -1- 1+ xx- eik|x|1-n|xx| j(x') = 4p-------|x--x'|-------------4p---| |x| x2 |m eik|x integral ( nx') ' | = |-0----- d3x' 1+ --- e-iknxj(x') | -4p-|x|------------|x-------------

(7.1)

In der Fernzone gilt:

|----------- integral --------------| | m0-eik|x- 3 ' -iknx' ' | |A = 4p |x| d x e j(x )| ----------------------------

Somit hängt das Integral nicht mehr von ab. Außerdem gilt durch Entwicklung der Exponentialfunktion:

e-iknx'= 1 - iknx'

In der Dipol-Näherung geht dies gegen -ik'.

|------------------- integral ------------| | m0eik|x| 3 ' ' | |A(x) = 4p |x|(- ik). d x(n .x)j | ----------------------------------

Wir wollen nun dieses Integral auswerten. Dazu formen wir um:

( ) [ ( ) ] (n .x')j = 1 x'× j × n + 1 (n.x')j + n .j x' 2---- ----- 2-------- --------- antisymmetrisch bez¨uglich x'<-->j symmetrisch bez¨uglich x'<--> j

1.Term: Magnetische Dipolstrahlung $|----------ik|x|-------------------- integral ------------| |A(x) = m0-e--(ik)(n × m) mit m = 1 dx'x'× j(x')| -------4p--|x|--------------------2---------------$
Erinnerung an Magnetostatik
2.Term: Elektrische Quadrupolstrahlung