Jedem Raumpunkt wird eine physikalische Größe zugeordnet. Diese Abbildung nennt man Feld. Nach dem Verhalten unter Koordinatentransformation unterscheidet man Skalar-, Vektor- und Tensorfelder (hier 3 Raumdimensionen).
Koordinatentransformation:
Dik beschreibt hierbei die Drehung/Spiegelung und yi die Verschiebung.
Die Umkehrabbildung lautet:
Wenn D eine orthogonale Transformation ist, gilt:
Beispiel:
- Skalare Felder
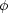 (
(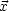 )
)
- Temperatur
- Druck
- Ladungsdichte
- Potential
Einschub: Einsteinsche Summationskonvention:
Man summiert immer über den Index, der gleich ist. Somit gilt nun:
Vektorfelder A(x):
- Elektrisches Feld
- Magnetisches Feld
- Vektorpotential
- Stromdichte
Tensorfeld Tij(x):
- Mechanischer Spannungstensor im festen Körper
- Feldstärke-Tensor im Minkowski-Raum
Unter Spiegelung ![]()
![]()
![]() ' = -
' = -![]() ändern Vektoren ihr Vorzeichen.
ändern Vektoren ihr Vorzeichen.
Dies gilt aber nicht für Pseudovektoren wie beispielsweise ![]() oder
oder ![]() ×
×![]() (Drehimpuls).
(Drehimpuls).
Skalare Felder ändern sich nicht unter Spiegelungen. Es gibt aber Pseudoskalare:
Verallgemeinerung: Tensor n-ter Stufe:
Wir betrachten einen antisymmetrischen Tensor:
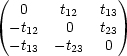
Diesen Tensor kann man mit einem Pseudovektor in Beziehung bringen:
- Gradient:
Der Gradient ist folgendermaßen definiert:
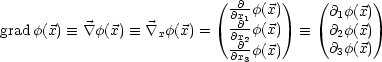
Der Gradient hat nun folgende wichtige Eigenschaften:
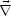
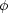 (
(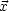 )
transformiert sich wie ein Vektor, wenn
)
transformiert sich wie ein Vektor, wenn 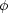 (
(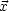 ) sich wie ein Skalar
transformiert. Wir wollen diese Aussage kurz beweisen:
) sich wie ein Skalar
transformiert. Wir wollen diese Aussage kurz beweisen:
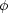 (
(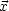 + d
+ d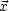 ) -
) - 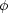 (
(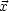 ) wobei d
) wobei d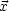 =
= 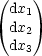 ein kleiner endlicher Vektor
beliebiger Richtung ist. Durch Taylorentwicklung erhalten wir:
ein kleiner endlicher Vektor
beliebiger Richtung ist. Durch Taylorentwicklung erhalten wir:
Aus hier gibt es einen Integralsatz: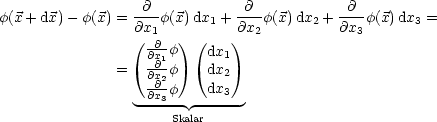
(2.1) 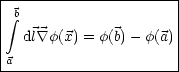
- Divergenz:
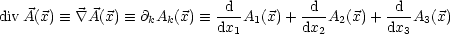
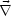 .
.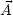 ist ein Skalar, da A'k(
ist ein Skalar, da A'k(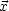 ') = D
kk'Ak'(
') = D
kk'Ak'(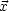 ).
).
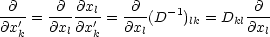
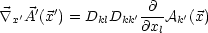
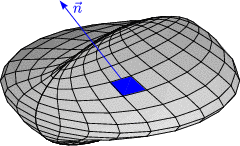
Das Flächenintegral über ein Vektorfeld
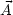 ist definiert durch:
ist definiert durch:
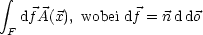
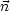 steht senkrecht auf der Fläche und ist bei geschlossener Fläche nach
außen orientiert, d
steht senkrecht auf der Fläche und ist bei geschlossener Fläche nach
außen orientiert, d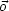 ist durch die Fläche von d
ist durch die Fläche von d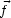 gegeben.
gegeben.
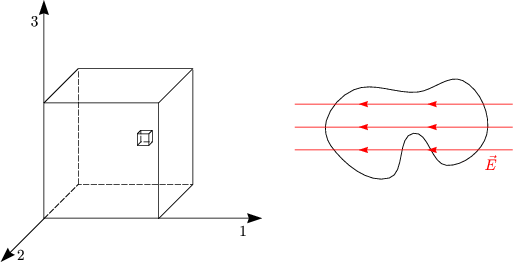
Wir leiten den Gaußschen Integralsatz her, welcher einen Zusammenhang zwischen div A und einem Flächenintegral herstellt. Dazu betrachten wir einen kleinen Würfel am Punkt
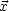 :
:
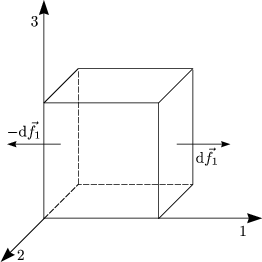
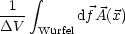
df steht senkrecht auf der Oberfläche. Der Betrag von d
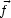 1 und d
1 und d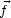 1'
lautet:
1'
lautet:
![-----1-----[A (x + Dx ,x,x )- A (x ,x ,x )] ds = @A1-(x ,x ,x )
Dx1Dx2Dx3 -1--1-----1--2-3-----1-1--2--3- @x1 1 2 3
@A1- Dx2Dx3
@x1 (x1,x2,x3)Dx1](th78x.gif)
Es handelt sich um 6 Flächen:
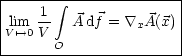
Für endliche Volumina gilt:
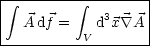
Dies ist der Gaußsche Integralsatz.
Beweisskizze:
Zerlege V in kleine Teilvolumina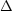 V . Die Beträge der
inneren Fläche heben sich weg, die der äußeren bleiben.
V . Die Beträge der
inneren Fläche heben sich weg, die der äußeren bleiben.
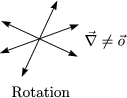
Ein Beispiel dafür ist eine Wasserströmung ohne Quellen.
- Rotation:
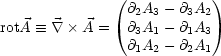
Behauptung:
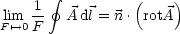
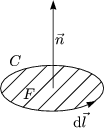
 sei die Normale auf der Fläche (Rechtsschraube mit C). Wir beweisen
diesen sogenannten Stokesschen Satz. Dazu betrachten wir folgende
Fläche:
sei die Normale auf der Fläche (Rechtsschraube mit C). Wir beweisen
diesen sogenannten Stokesschen Satz. Dazu betrachten wir folgende
Fläche:
![gf
lim 1- A dl =
F'-->0 F (
x2 integral +Dx2 x3 integral +Dx3
= ---1----. dx'2 .A2(x1,x'2,x3) + dx'3(x1,x2 + Dx2, x'3)-
Dx2Dx3- x2 x3
F
x2+ integral Dx2 x3+ integral Dx3 )
+ dx'2A(x1,x'2x3 + Dx3)- dx'3A(x1,x2,x'3) =
x2 x3
( x2+Dx2
---1---- integral ' ' '
= Dx2Dx3 . dx2[A2 (x1,x2,x3)- A2 (x1,x 2,x3 + Dx3)]+
x2
x3+ integral Dx3 )
+ dx'3 [A3 (x1,x2 + Dx2,x'3)- A3(x1,x2,x'3)] =
x
[ (3 ) ( ) ]
= ---1---- Dx2 - -@-A2 Dx3 + Dx3 -@--A3 Dx2 =
Dx2Dx3 @x(3 ) @x2
= -@--A - -@--A = rotA
@x2 3 @x3 2 1](th88x.gif)
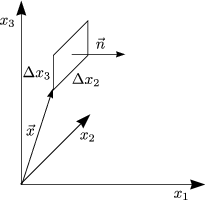
(2.2) 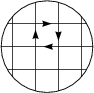 Durch Zerlegung einer endlichen Fläche F in kleine Elemente df und
Summation über alle Beiträge (wobei sich bei den Linienintegralen die
inneren Anteile kompensieren) erhalten wir:
Durch Zerlegung einer endlichen Fläche F in kleine Elemente df und
Summation über alle Beiträge (wobei sich bei den Linienintegralen die
inneren Anteile kompensieren) erhalten wir:
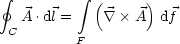
Damit haben wir den Satz von Stokes.