8.1 Zeitlich gemittelte Gren

8.1 Zeitlich gemittelte Größen

Für eine physikalische Größe gilt folgender Zusammenhang mit der mathematischen komplexen Größe:

( ) 1( -iwt * +iwt) Ephys = Re E = 2 E(x)e + E (x)e

( ) ( ) Bphys = Re B = 1 B(x)e-iwt + B*(x)e+iwt 2

Für die Energieflußdichte gilt:

|------------------| | -1- | S = m0Ephys× Bphys | --------------------

Wir interessieren uns nun für zeitlich gemittelte Größen.

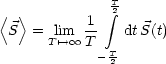
integral T2 <S> = lim -1 dtS(t) T'--> oo T -T2

Es tauchen hier folgende Integrale auf:

_-e^-it ^. e^+it dt = 1
_-e^-2it = T0

Nun gilt:

< > 1-1 ( * * ) -1- ( * ) S = m04 . E(x × B (x)+ E (x ×B(x) = 2m0 Re E(x) × B (x)

Fluß durch Kugeloberfläche::

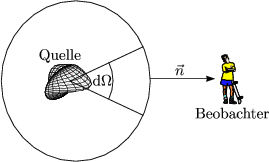
Die abgestrahlte Leistung durch die Oberfläche ist gegeben durch:

integral integral integral P = dF S = S .n df = S .n .|x |2d_O_

Für die Leistung in einem bestimmten Raumwinkel gilt:

dP- = |x|2 .S .n d_O_

Wir wenden dies auf die Dipolstrahlung an:

dP 1 ( ) 1 (m ck2)2 ( ) --- = ---Re E(x)× B*(x) .nx2 = ---x2 -0--- c.Re [(n× p)× n]× [n× p]* .n d_O_ 2m0 2m0 4p|x|

Uns hilft bei dieser Menge an Kreuzprodukten die Grassmann-Formel weiter:

[ ] ( ) a × b × c = b(ac)- c ab

Damit gilt dann:

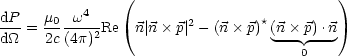
( ) dP- m0-w4-- 2 * d_O_ = 2c(4p)2Re n|n× p| - (n× p) (n×-p).n 0

Nun folgt schlußendlich:

|---------4--------| dP- = m0-w--|n × p| 2 | d_O_---4p-8pc---------

Anwendung auf E1-Strahlung:

|------------------| dP m0 w4 2 | d_O_ = 4p-8pc-|n × p| | --------------------

Wir machen nun die Annahme, daß reell sei. Es handelt sich dann um eine ganz besondere Form des Dipols; die Ladung oszilliert linear in eine bestimmte Richtung. Es gilt für den Betrag eines Kreuzproduktes:

|a× b|= |a|.|b ||sin h|

Damit folgt dann:

dP-= m0-w4-|p| 2sin2h d_O_ 4p 8pc

ist der Winkel zwischen Dipolrichtung und Beobachter-Richtung.

integral 4 integral |-----4---| P = d_O_ dP-= m0-w--| p|2 d_O_ .sin2 h= |-m0-w-|p|2| d_O_ 4p 8pc ---- ---- -12p-c----- 2p.43

Drei einfache Beispiele:

Wir betrachten einen linearen oszillierenden Dipol. Die zeitliche Ladungsverteilung sehe folgendermaßen aus:

$(0 ) x = a- 0 cos(wt) + 2 1$

$x- = -x+$

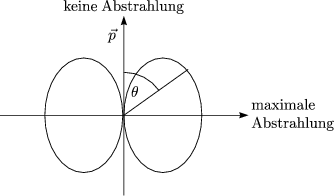
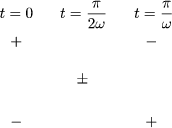
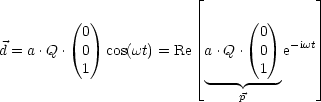
$|_ _| (0 ) (0) d = a .Q. 0 cos(wt) = Re a .Q . 0 e-iwt 1 |_ 1 _| ---- ---- p$
Es handelt sich um eine lineare Polarisation, denn × ~ ist reell und _phys(,t) ~ ×cos(t).
Ein in der x-y-Ebene rotierender Dipol

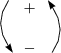
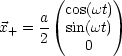
$( ) a cos(wt) x+ = 2- sin(wt) 0$

$x- = -x+$

$( ) |_ ( ) _| cos(wt) e-iwt d = Q .a. sin(wt) = Re |_ a .Q . ie- iwt _| 0 0$
Somit folgt:
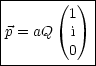
$|-----------| | (1 ) | |p = aQ i | | 0 | ------------$
Dies führt somit zu einer zirkularen Polarisation in z-Richtung. In z-Richtung ist:
$( ) ( ) ( ) 0 1 -i b ~ n× p ~ 0 × i = 1 1 0 0$

$|_ ( -ie-iwt)_ | ( - sin(wt)) B(x,t) ~ Re |_ e-iwt _| = cos(wt) 0 0$
Es stellt sich nun die Frage, was sich für den Beobachter in x- bzw. y-Richtung ergibt.
Lineare Antenne
Für den Strom gilt:

$( ) -iwt 2| z| -iwt I(z,t) = I(z)e = I0 1 - d e$
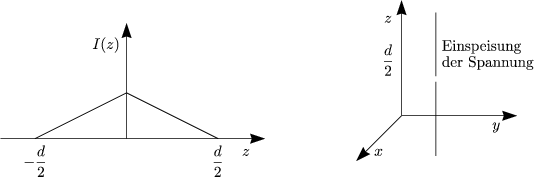
Die Ladung pro Längeneinheit ergibt sich aus der Kontinuitätsgleichung:
$r = -1 ( \~/ j), \~/ j ==>-dI(z) iw dz$

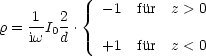
$1 2 { - 1 f¨ur z > 0 r =--I0- . iw d +1 f¨ur z < 0$

$2iI0 r(z) = ± wd$

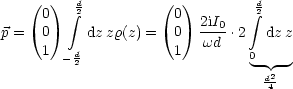
$( ) integral d2 ( ) integral d2 0 0 2iI0- p = 0 dzzr(z) = 0 wd .2 dzz 1 -d2 1 0---- d42$

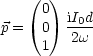
$(0) p = 0 iI0d- 1 2w$
Für die abgestrahlte Leistung gilt:
$|-------------| | m0w2d2I20 | -P-=---48pc---|$

[next] [front] [up]