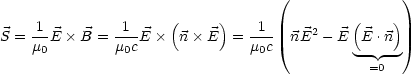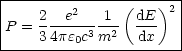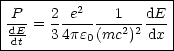8.2 Abstrahlung von einer bewegten Punktladung
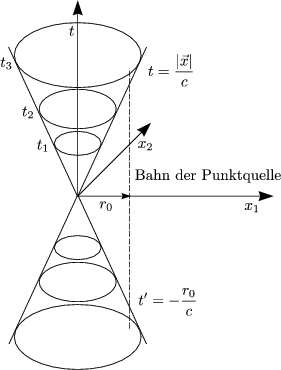
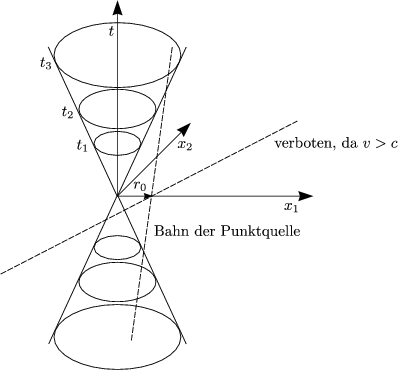
Beispiel für retardierten Aufpunkt:
Der Beobachter sei bei 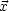 = 0, t = 0.
= 0, t = 0.
Wir wollen nun die  -Funktion in Gleichung (*) auswerten.
-Funktion in Gleichung (*) auswerten.
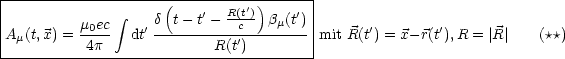
Wir erinnern uns dabei an die Eigenschaften der  -Funktion:
-Funktion:
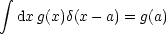
Haben wir innerhalb der  -Funktion eine stetige Funktion f(x), so folgt:
-Funktion eine stetige Funktion f(x), so folgt:
![integral ----------------[---------]-----|
| dxg(x)d(f(x)) = -'1--g(x) |
-------------------|f-(x)|----f(x)=0-](th1454x.gif)
Wir wenden diese Beziehung auf unser Beispiel an:

Wir wollen dies beweisen:


Damit gilt dann:
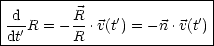
Damit folgt also:

t' ist die retardierte Zeit. Diese Gleichung läuft unter dem Namen
Lienard-Wichert-Potential______________________. Wir haben hier die relativistische Verallgemeinerung der
Formeln der Potentiale, die wir zu Anfang der Vorlesung diskutiert hatten. Aus
Gleichung (***) können nun die Felder berechnet werden. Etwas bequemer geht dies
auch mit Gleichung (**).
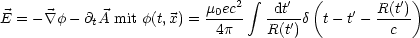

Die 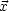 -Abhängigkeit steckt in R = |
-Abhängigkeit steckt in R = | -
- (t')|. Damit folgt für den Gradienten mittels
Kettenregel:
(t')|. Damit folgt für den Gradienten mittels
Kettenregel:

Die genaue Rechnung findet man im Jackson:
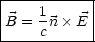
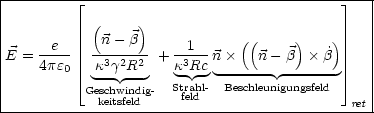
Für das Geschwindigkeitsfeld folgt:
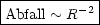
Für das Strahlfeld folgt:
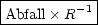

Spezialfälle entstehen für:
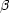 = 0
= 0
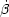 = 0
= 0
Der Grenzfall für nichtrelativistische Bewegung (|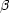 |« 1) folgt mit:
|« 1) folgt mit:


Für das Beschleunigungsfeld folgt:
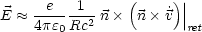
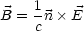
Für den Energiefluß (Poynting-Vektor) in der Strahlungszone folgt:
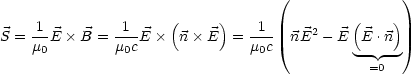
Für die abgestrahlte Leistung pro Raumwinkel folgt:

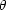 ist hierbei der Winkel zwischen
ist hierbei der Winkel zwischen 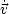 und
und 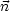 .
.  ist zur retardierten Zeit zu nehmen. Für
die totale abgestrahlte Leistung folgt durch Integration über den gesamten
Winkel:
ist zur retardierten Zeit zu nehmen. Für
die totale abgestrahlte Leistung folgt durch Integration über den gesamten
Winkel:
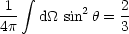
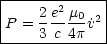
Dies ist die sogenannte Larmor-Formel.
Übungsaufgabe: Oszillierende Ladung
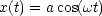
Es soll die Leistung P berechnet werden.
Übergang zum relativistischen Resultat (ohne Herleitung):
![|------------[-------------]|
| 2--e2- 6 ˙2 ( ˙)2 |
|P = 34pe0cg b - b ×b |
-----------------------------](th1484x.gif)
![]() (t) mit der
Geschwindigkeit
(t) mit der
Geschwindigkeit ![]() (t) =
(t) = ![]()
![]() (t) =
(t) = ![]() (t) und der Beschleunigung
(t) und der Beschleunigung ![]() (t) =
(t) = ![]() (t).
Für den Beobachter bei
(t).
Für den Beobachter bei ![]() = 0 und t = 0 ist das von der Punktladung bei
den retardierten Koordinaten erzeugte Potential relevant.
= 0 und t = 0 ist das von der Punktladung bei
den retardierten Koordinaten erzeugte Potential relevant.
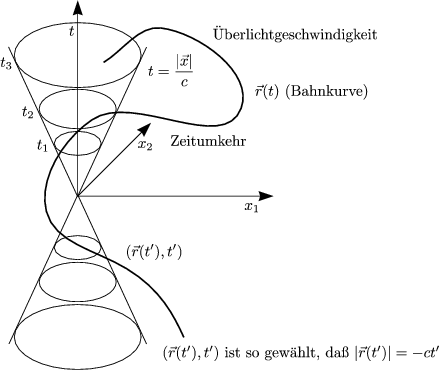
![]() (t,
(t,![]() ) berechnen. Dazu verwenden wir wieder die
retardierten Potentiale.
) berechnen. Dazu verwenden wir wieder die
retardierten Potentiale. 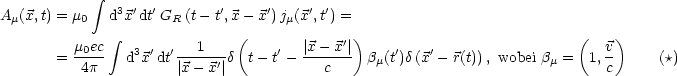
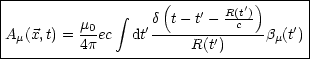
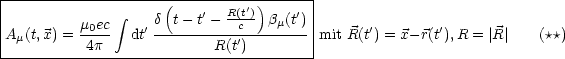
![integral ----------------[---------]-----|
| dxg(x)d(f(x)) = -'1--g(x) |
-------------------|f-(x)|----f(x)=0-](th1454x.gif)