3.1 Energie des statischen Feldes

Durch Benutzung der Poisson-Gleichung folgte:

² nannten wir die Energiedichte des elektrischen Feldes. Nun betrachten wir zwei entgegengesetzt gleiche Ladungen. Dann folgt:

Andererseits gilt aber auch ² > 0, woraus dann folgt:

Der Unterschied zwischen U_ww und U liegt in den positiven „Selbstenergiebeiträgen“.

Beispiel:

Dann gilt:

Nun folgt für die Energie:

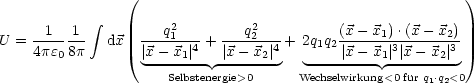
Die ersten beiden Terme sind größer 0 (das Integral divergiert), das Integral über den dritten Term liefert:

Dies kann man durch explizite Berechnung zeigen oder auch so:

Durch partielle Integration erhalten wir:

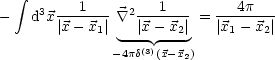
Für die Berechnung der Kräfte zwischen den Ladungen ist nur der zweite Term relevant.

Beispiel für Energiedichte:

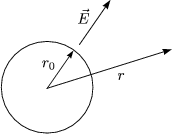
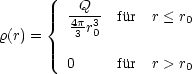
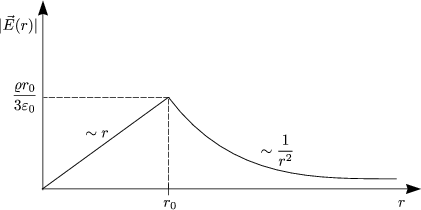
Gesucht ist nun das Feld E. Wir verwenden den Gaußschen Satz und erhalten:

Sei V Kugel mit Radius r und F die zugehörige Oberfläche:

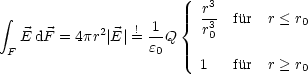
Dies können wir jetzt auflösen und erhalten:

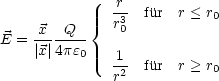
Die Feldenergie ergibt sich jetzt als:

Klassischer Elektronenradius: