[next] [prev] [prev-tail] [tail] [up]

3.2 Oberflächenladungen

Auf einer Fläche S sei eine Ladung mit der Flächendichte s(x) gegeben, mit der Eigenschaft:

integral integral dxr(x) = df s(x) V F

PIC

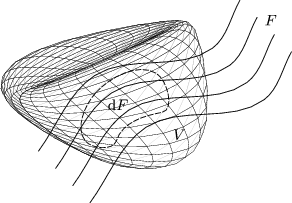
F beschreibt dabei den im Integrationsgebiet V gelegenen Teil der Fläche S. Wir interessieren uns nun für die Änderung des elektrischen Feldes beim Durchgang durch S.

PIC

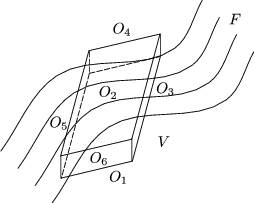
O1, O2 sind die gegenüberliegenden großen Flächen. Mit O3, O4, O5 und O6 werden die schmalen Streifen bezeichnet. Daraus folgt nun:

O = O + O + O + O + O + O 1 2 3 4 5 6

Nach dem Gaußschen Satz gilt:

integral integral E dF = 1- d3xr(x) = 1- dfs(x) e0 e0O1 O V

Die Beiträge von O3,4,5,6 sind vernachlässigbar, da man die Streifen sehr klein machen kann. Für die Anteile von O1 und O2 gilt nun, daß ihre Flächennormalen entgegengesetzt gleich sind.

PIC

integral integral ( ) 1- integral E dF = E2n - E1n df = e0 dfs(x) O O1 O1

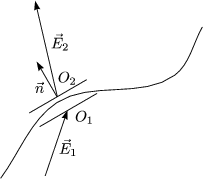
Also folgt:

integral ( ) 1 integral E2 - E1 n df = -- s(x)df f¨ur beliebige O1 O1 e0O1

Daraus folgt also:

(E2(x)- E1(x)).n = 1-s(x) e0

Wir haben somit einen Sprung an der Komponente senkrecht zur Fläche. Komponenten parallel zur Fläche sind stetig.

Der Beweis erfolgt über den Stokesschen Satz, indem man über eine geschlossene Fläche integriert:

\~/ × E = o

Wir gehen nun zum Potential über, falls Raum- und Flächenladungen vorliegen:

|----------- integral ---------------- integral ----------| |f(x) =--1- d3x-r(x')--+ -1-- df-s(x')-| -------4pe0------|x--x'|--4pe0-----|x--x'||

[next] [prev] [prev-tail] [front] [up]