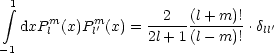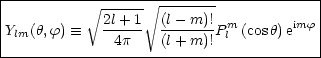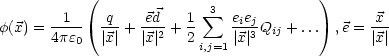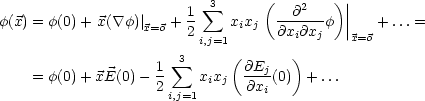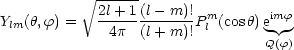3.3 Randwertprobleme in der Elektrostatik
- Leiter:
In einem Leiter befinden sich leicht bewegliche Ladungsträger
(Elektronen). Falls im Innern des Leiters ein elektrisches Feld existiert,
führt dies zu einem Strom von Elektronen bis zur Kompensation des Feldes
durch Oberflächenladungen.
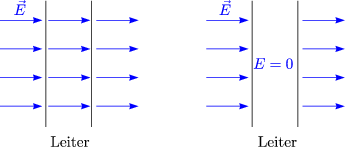
Ein Leiter ist somit ein Gebiet ohne Feld (mit konstantem Potential).
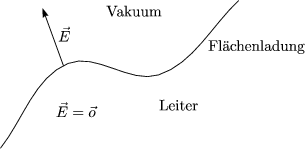
Es gibt einen Sprung in der Komponente senkrecht zur Oberfläche. Die
parallel zur Oberfläche laufende Komponente ist stetig. Das im Innern des
Leiters 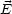 =
= 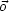 ist, muß
ist, muß 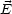 im Außenraum senkrecht zur Fläche stehen.
im Außenraum senkrecht zur Fläche stehen.

Die Oberfläche des Leiters stellt somit eine Äquipotentialfläche dar. Ein
Beispiel dafür ist der Hohlraum in einem Leiter:

Es gilt somit  =const. im inneren Rand des Leiters. Falls sich
keine Ladungen im Inneren befinden, ist dies die einzige Lösung der
Laplace-Gleichung:
=const. im inneren Rand des Leiters. Falls sich
keine Ladungen im Inneren befinden, ist dies die einzige Lösung der
Laplace-Gleichung:  ist somit konstant im Innern, womit gilt
ist somit konstant im Innern, womit gilt 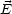 =
= 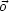 . Dies
gilt im Innern auch bei Anwesenheit von Ladungen im Außenraum. Die
Ladungsträger richten sich so aus, daß sie das Feld im Innern abschirmen.
Dies ist also nichts anderes als ein Faradayscher Käfig. Zusammenfassend
kann man also sagen: Das Potential im Leiter ist konstant und das
elektrische Feld somit 0.
. Dies
gilt im Innern auch bei Anwesenheit von Ladungen im Außenraum. Die
Ladungsträger richten sich so aus, daß sie das Feld im Innern abschirmen.
Dies ist also nichts anderes als ein Faradayscher Käfig. Zusammenfassend
kann man also sagen: Das Potential im Leiter ist konstant und das
elektrische Feld somit 0.

Der Vektor des 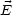 -Feldes steht senkrecht auf der Oberfläche. Die
Flächenladungsdichte
-Feldes steht senkrecht auf der Oberfläche. Die
Flächenladungsdichte  ist:
ist:
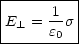
Beim allgemeinen Problembereich handelt
es sich um partielle Differentialgleichungen mit Randwertproblemen, hier
speziell die Poisson-Gleichung:
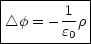
Bisher war es so, daß das Potential  im Unendlichen gegen 0 ging.
Im folgenden werden aber Probleme behandelt, die Randbedingungen im
Endlichen, wie beispielsweise auf Flächen, aufweisen.
im Unendlichen gegen 0 ging.
Im folgenden werden aber Probleme behandelt, die Randbedingungen im
Endlichen, wie beispielsweise auf Flächen, aufweisen.
- Methode der Spiegelladungen
- Geerdete Halbebene; x = 0
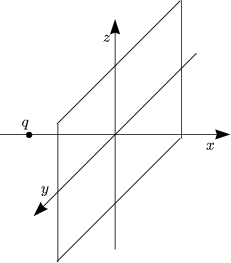
Eine Ladung q befindet sich bei x = -d; y = z = 0. Wir bestimmen
das Feld im Halbraum, also für x < 0.
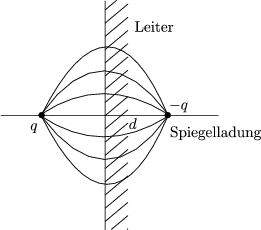
Es wird gefordert, daß  bei x = 0 senkrecht auf der Ebene steht.
bei x = 0 senkrecht auf der Ebene steht.  muß
im Bereich x < 0 die Poisson-Gleichung erfüllen. Das Feld im Halbraum
x < 0 wird durch Ladung und Spiegelladung beschrieben. Mögliche
Fragestellungen sind daher:
muß
im Bereich x < 0 die Poisson-Gleichung erfüllen. Das Feld im Halbraum
x < 0 wird durch Ladung und Spiegelladung beschrieben. Mögliche
Fragestellungen sind daher:
- Flächenladungsverteilung im Leiter
- Induzierte Gesamtladung (-q')
- Berechne die auf q ausgeübte Kraft
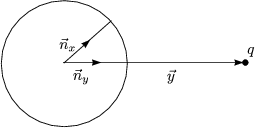
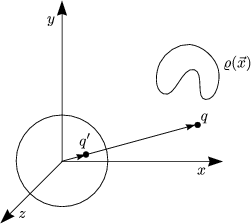
- Geerdete Metallkugel (Radius a) und Punktladung q außerhalb am Punkt
 :
:
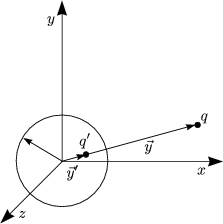
Wir suchen die Bildladung q’ am Ort  ’ im Innern der Kugel, so daß
’ im Innern der Kugel, so daß
 |
| |=a = 0 ist. Wir verwenden den Ansatz (Ursprung im Mittelpunkt der
Kugel):
|=a = 0 ist. Wir verwenden den Ansatz (Ursprung im Mittelpunkt der
Kugel):

Es wird definiert:

Aus Symmetriegründen gilt 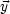 ' = y'
' = y' y. Außerdem fordern wir aufgrund der
Erdung:
y. Außerdem fordern wir aufgrund der
Erdung:
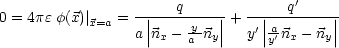
Die Lösung des Problems ist:
Analoge Beispiele:
- Kugel mit vorgegebener Ladung Q (nicht geerdet)
- 2 Halbkugeln auf verschiedenem Potential
- Sich schneidende leitende Ebenen

3.3.1 Green’sche Funktionen und ihre Anwendungen
Ziel:
- Berechnung von
 im Gebiet V aus vorgegebenen
im Gebiet V aus vorgegebenen 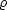 in V und dem Potential
in V und dem Potential
 (oder seiner Ableitung) am Rand
(oder seiner Ableitung) am Rand
- Mathematischer Einschub: Green’sches Theorem
Wir erinnern an den Gaußschen Satz:

Wir wählen jetzt ein bestimmtes  (
( ) =
) =  (
( )
)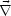
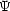 (
( ), wobei
), wobei  und
und 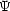 zunächst beliebige Skalarfelder sind. Nun folgt:
zunächst beliebige Skalarfelder sind. Nun folgt:
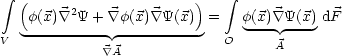
Nun wird die entsprechende Gleichung subtrahiert, bei der  und
und  vertauscht sind:
vertauscht sind:

Dies ist das sogenannte Green’sche Theorem. Oft schreibt man in
Lehrbüchern für 
 (
( )d
)d


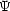 (
( )dF
)dF 

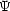 (
( )dF.
)dF.
- Green’sche Funktion
Gegeben sei V mit Rand O,  (oder alternativ
(oder alternativ 
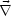
 ) auf O vorgegeben
(Randbedingungen), sowie die Quellen
) auf O vorgegeben
(Randbedingungen), sowie die Quellen 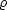 in V . Bestimme
in V . Bestimme  . Dies nennt
man „Dirichlet-Randproblem“. (Wenn
. Dies nennt
man „Dirichlet-Randproblem“. (Wenn 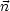

 vorgeben ist, handelt es sich
um das Neumann-Randproblem.) Wir suchen G(
vorgeben ist, handelt es sich
um das Neumann-Randproblem.) Wir suchen G( ,
,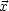 ') für welches für
') für welches für 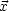 ,
,
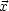 '
'  V gilt:
V gilt:
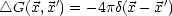
Dann kann G zerlegt werden in G(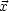 ,
,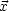 ') =
') = 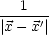 + F(
+ F( ,
, ') und
') und
 F(
F(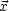 ,
,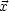 ') = 0.
') = 0.
Beispiel:
Wenn  = 0 auf Kugeloberfläche festgelegt ist, dann ist
F(
= 0 auf Kugeloberfläche festgelegt ist, dann ist
F( ,
,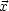 ') = -
') = -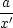
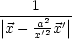 . Verwende Green’sches Theorem mit
. Verwende Green’sches Theorem mit 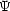 (
( ') = G(
') = G(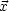 ,
, ')
und
')
und  ' als Integrationsvariable.
' als Integrationsvariable.

Nun schreiben wir das Potential als:
![|-----------------------------------------------------------------------|
| 1 integral ' ' ' 1 integral '[ ' ' ' '] |
|f(x) = 4pe0 dx G(x,x)r(x )- 4p- dF f(x ) \~/ x'G(x, x)- G(x,x ). \~/ x'f(x )|
------------V-------------------O---------------------------------------](th316x.gif)
- Dirichlet-Randwertproblem
 sei auf O vorgegeben. Suche GD so, daß GD(
sei auf O vorgegeben. Suche GD so, daß GD(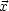 ,
,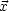 ') = 0 für
') = 0 für
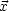 '
'  O und natürlich weiter
O und natürlich weiter  G(
G( ,
,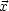 ') = -4
') = -4
 (
( -
- '). Das legt G
D
eindeutig fest (ohne Beweis)! Dann folgt daraus:
'). Das legt G
D
eindeutig fest (ohne Beweis)! Dann folgt daraus:
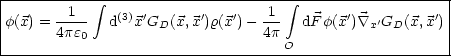
Falls 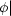 O = 0 (geerdeter Leiter), so trägt nur der erste Term bei.
Der wichtige Punkt ist folgender, daß GD nur von der Geometrie
(V , O) und der Art der Randbedingung (Dirichlet oder Neumann)
abhängt, aber nicht von
O = 0 (geerdeter Leiter), so trägt nur der erste Term bei.
Der wichtige Punkt ist folgender, daß GD nur von der Geometrie
(V , O) und der Art der Randbedingung (Dirichlet oder Neumann)
abhängt, aber nicht von 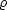 und
und 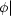 O.
O.
Anmerkung:
GD ist symmetrisch, d.h. GD( ,
,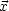 ') = G
D(
') = G
D( ',
', ). Wir
beweisen dies über das Green’sche Theorem mit
). Wir
beweisen dies über das Green’sche Theorem mit  (
( ) = GD(
) = GD( ,
, ''),
''),
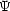 (
(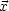 ) = GD(
) = GD( ',
',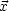 '') und
'') und 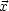 '' als Integrationsvariable.
'' als Integrationsvariable.
![( ) ( )
integral
d(3)x'' GD(x,x'') /_\ x''GD(x',x'') - / _\ x'GD(x,x'')GD(x',x'') =
V ----- ----- ----- -----
integral [( -4pd(x'-x'')) ( -4pd(x-x'') )]
= dF '' G (x,x'')-@--G(x',x'') - --@-G (x,x'').G (x',x'')
D @n'' @n'' D D
O](th338x.gif) | (3.1) |
Das Integral über die Oberfläche O ist 0, da die Greenfunktion
auf der Oberfläche den Wert 0 annimmt. Daraus folgt dann die
Symmetrie:
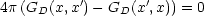
Interpretation von F:
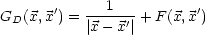

F ist ein Potential, welches so gewählt wird, daß die Wirkung einer
Punktladung bei  ' gerade kompensiert wird.
' gerade kompensiert wird.
- Neumann-Randwertproblem
Wir nehmen an, daß  O gegeben sei, d.h. daß die Feldstärke
senkrecht zur Oberfläche gegeben ist.
O gegeben sei, d.h. daß die Feldstärke
senkrecht zur Oberfläche gegeben ist. 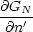 = 0 wäre auf den ersten Blick
eine mögliche Lösung, aber es gilt:
= 0 wäre auf den ersten Blick
eine mögliche Lösung, aber es gilt:

dF'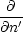 GN(
GN( ,
,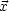 ') muß infolgedessen -4
') muß infolgedessen -4 sein. G
N(
sein. G
N( ,
,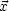 ') wird deswegen so
gesucht, daß gilt:
') wird deswegen so
gesucht, daß gilt:

Daraus folgt:

Beispiel für Dirichlet-Problem:
Das Potential  sei auf der Kugeloberfläche
vorgegeben. Wir suchen nun G(
sei auf der Kugeloberfläche
vorgegeben. Wir suchen nun G( ,
, ') so, daß folgende Bedingungen erfüllt
sind:
') so, daß folgende Bedingungen erfüllt
sind:
 G(
G(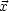 ,
,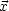 ') = -4
') = -4
 (
(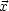 -
- ')
')
- G(
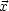 ,
,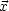 ') = 0 für |
') = 0 für | | = a
| = a
Die Lösung ist gegeben durch das Potential einer Punktladung am Punkt  in
Anwesenheit einer geerdeten Kugel mit festem a um den Nullpunkt.
in
Anwesenheit einer geerdeten Kugel mit festem a um den Nullpunkt.

Dies kann man nun auch schreiben als:

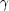 ist hierbei der Winkel zwischen den Vektoren
ist hierbei der Winkel zwischen den Vektoren  und
und 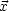 '. Sie Symmetrie zwischen
'. Sie Symmetrie zwischen 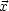 ,
,
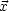 ' ist hier offensichtlich.
' ist hier offensichtlich.
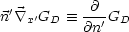
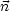 ist aus dem Volumen V nach außen gerichtet, also:
ist aus dem Volumen V nach außen gerichtet, also:

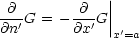
Somit folgt, wie man durch Nachrechnen überprüfen kann:
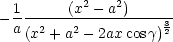
Für vorgegebenes Potential  (a,
(a,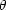 ,
, ) in Kugelkoordinaten auf Kugeloberfläche
erhält man im Außenraum (ohne zusätzliche Ladung):
) in Kugelkoordinaten auf Kugeloberfläche
erhält man im Außenraum (ohne zusätzliche Ladung):
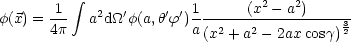

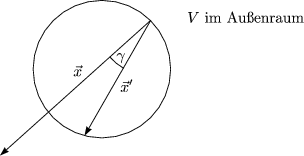

Mittels des Skalarprodukts und der obigen Beziehungen folgt:

3.3.2 Laplace-Gleichung mit Randwerten auf Quader/Separation der
Variablen
- Karthesische Koordinaten
Wir machen einen Ansatz:

In die Differentialgleichung eingesetzt, folgt:

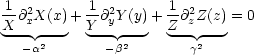
Jeder Term sei konstant.

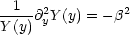
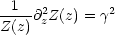
Diese Konstanten müssen nun folgende Beziehungen erfüllen:
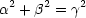
Die Lösung ist nun, da die zweite Ableitung einer Exponentialfunktion
wieder eine Exponentialfunktion ist:
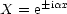
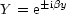

Die Lösung von (*) ist X . Y . Z und beliebige Linearkombination.
Wir wählen nun die Linearkombination und  ,
, 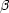 ,
, 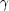 so, daß die
Randbedingungen erfüllt werden.
so, daß die
Randbedingungen erfüllt werden.
Beispiel:
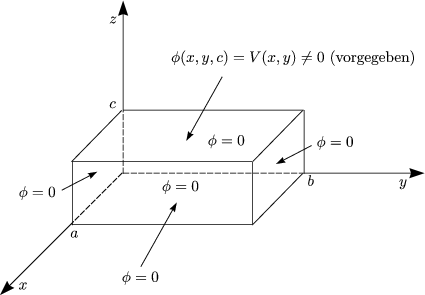
 sei somit gleich null auf fünf Flächen. Zuerst berücksichtigen wir die drei
Flächen durch den Ursprung:
sei somit gleich null auf fünf Flächen. Zuerst berücksichtigen wir die drei
Flächen durch den Ursprung:
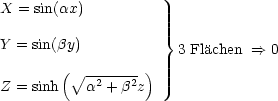


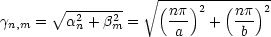
Daraus folgt nun das Potential:
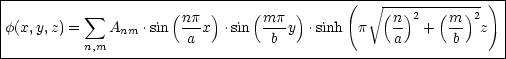
 erfüllt die Randbedingungen
erfüllt die Randbedingungen  = 0 auf 5 Flächen. Die sechste Randbedingung
ist bei z = c:
= 0 auf 5 Flächen. Die sechste Randbedingung
ist bei z = c:

Die Anm werden nun „passend“ gewählt.
Forderung:
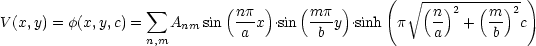
Wir stellen V (x,y) mittels einer Fourier-Reihe dar. V wird mit folgenden
Koeffizienten entwickelt:

Wir bestimmen Anm:



3.3.3 Mathematischer Einschub:Orthogonale Funktionen, Entwicklungen,
Fourier-Reihen
Wir erinnern uns an die lineare Algebra (vollständige Orthonormalbasis
{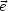 i}):
i}):
 i
i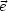 j =
j =  ij
ij
- Der Vektorraum wird aufgespannt durch
 i
i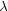 i
i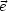 i, wobei
i, wobei 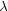 i beliebig
ist.
i beliebig
ist.
Jeder Vektor  kann dargestellt werden durch:
kann dargestellt werden durch:

Die Komponenten vi sind gegeben durch vi = 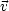
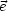 i, d.h. wir entwickeln
i, d.h. wir entwickeln  nach
der Basis {
nach
der Basis { i}. Analog entwickeln wir eine Funktion bezüglich einer Basis, d.h.
wir suchen eine Funktion beispielsweise durch Polynome oder durch
trigonometrische Funktionen.
i}. Analog entwickeln wir eine Funktion bezüglich einer Basis, d.h.
wir suchen eine Funktion beispielsweise durch Polynome oder durch
trigonometrische Funktionen.

Wir schreiben dies in Komponenten:

eki ist hierbei die k-te Komponente von 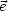 i. Es muß also folglich gelten:
i. Es muß also folglich gelten:
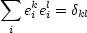
Dies ist die sogenannte Vollständigkeitsrelation. Wir probieren das für den
zweidimensionalen Raum aus:
- 1.Wahl:

- 2.Wahl:

Analog dazu entwickeln wir eine Funktion bezüglich eines Orthonormalsystems
(beispielsweise von Polynomen oder trigonometrischen Funktionen). Hieraus folgt die
Fourier-Entwicklung
_________________.
Durch Hinzunahme von immer mehr Funktionen kommt eine bessere Näherung
zustande. Forderungen an die Basisfunktionen sind nun:
Eine beliebige Funktion f( ) werde nun genähert durch:
) werde nun genähert durch:
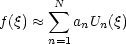
Wir fordern eine optimale Näherung, d.h. wir definieren MN als den Abstand der
Funktion von der Näherung:

Dieser Abstand sei minimal, so daß die Näherungsfunktion im Mittel möglichst nahe
an der Funktion f( ) liegt. Dann kann man zeigen, daß der Koeffizient an
folgendermaßen gegeben ist:
) liegt. Dann kann man zeigen, daß der Koeffizient an
folgendermaßen gegeben ist:
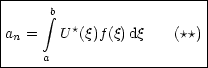
Den Beweis schlage man in einem Buch oder Skript der Höheren Mathematik
nach.
Das System ist „vollständig“, wenn MN 0 für N
0 für N
 . Dann schreiben
wir:
. Dann schreiben
wir:
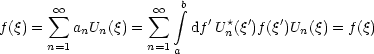
Wir vertauschen Integral und Summe:

Daraus folgt:
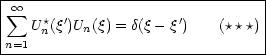
Jetzt haben wir unsere Vollständigkeitsrelation. Speziell im Intervall  gilt:
gilt:
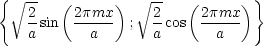
Falls m ganzzahlig ist, handelt es sich um eine vollständige Orthonormalbasis. Die
Fourier-Reihe von f(x) in  sei un gegeben durch:
sei un gegeben durch:
![|-------------------------------------------------|
| 1 sum oo [ (2pmx ) (2pmx )] |
|f(x) = 2 A0 + Am cos --a-- + Bm sin --a-- |
-------------m=1----------------------------------](th430x.gif)
Die Koeffizienten Am und Bm sind nun gegeben durch:

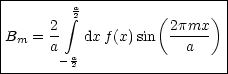
3.3.4 Laplace-Gleichung in Kugelkoordinaten

In Kugelkoordinaten lautet diese Gleichung:
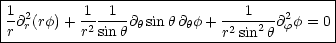
Hier treten keine gemischten Ableitungen auf, weil es sich beim Kugelkoordinatensystem
um ein Orthonormalsystem handelt. Wir substituieren:
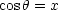
Die Substitutionsvariable x ist hier natürlich nicht gleich der karthesischen
Koordinaten x!
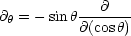

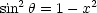
Wir suchen eine Produktdarstellung für  und führen eine Separation der Variablen
durch:
und führen eine Separation der Variablen
durch:

Für die Laplace-Gleichung folgt somit:

Wir dividieren durch ![[ ]
-1 .---1---U-.P .Q
r2 (1- x2) r](th441x.gif) :
:
![2 2 [1 2 1 1 @ 2 @ ] 1 2
r (1- x ) U-@rU + r2P-@x-(1- x )@xP + Q-@fQ = 0
----------------- ----------------- ----
h¨angt nicht von f ab hv¨anognt r n,xic ahbt](th442x.gif)
Bei den beiden Termen handelt es sich somit um Konstanten:
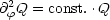
Daraus folgt nun die Lösung:
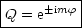
(Warum nicht e±
 ?) Q(
?) Q( ) muß eindeutig und stetig in (0,2
) muß eindeutig und stetig in (0,2 ) sein. m ist also
ganzzahlig. Wir erhalten somit:
) sein. m ist also
ganzzahlig. Wir erhalten somit:


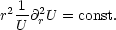
Die Lösung ist somit gleich:
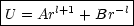
A, B, l sind zunächst beliebig. Wir leiten U zweimal nach r ab und erhalten:
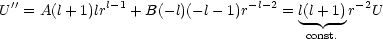
Die Gleichung für P lautet:

Dies ist die verallgemeinerte Legendre-Gleichung. Plm(x) sind die assoziierten
Legendre-Funktionen.
Forderung:
- Plm ist eindeutig in (-1,1).
- Die Funktion soll endlich und stetig sein.

Zunächst betrachten wir den Grenzfall für m = 0 (für Probleme mit azimuthaler
Symmetrie, unabhängig von  ):
):
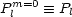
Pl sind die sogenannten Legendre-Polynome. Somit erhalten wir die
Legendre-Gleichung
________________:
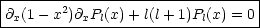
Wir haben hier die sogenannte Rodrigues-Formel vor uns. Pl sind Polynome der
Form (hier ohne Beweis):

Das Polynom hat den Grad l.
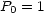
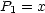
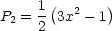
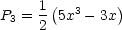
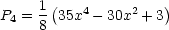
Die Polynome Pl bilden ein Orthogonalsystem, das heißt:

Die Normierung ist hier nicht 1, sondern  , wie wir sehen. Jede Funktion auf
<-1,1> kann durch
, wie wir sehen. Jede Funktion auf
<-1,1> kann durch  l = 0
l = 0 AlPl(x) genähert werden. Wir haben somit ein
Fundamentalsystem, welches ähnlich wie die Fourierreihe funktioniert. Es handelt
sich bei den Funktionen aber nicht um trigonometrische Funktionen, sondern um
Polynome.
AlPl(x) genähert werden. Wir haben somit ein
Fundamentalsystem, welches ähnlich wie die Fourierreihe funktioniert. Es handelt
sich bei den Funktionen aber nicht um trigonometrische Funktionen, sondern um
Polynome.
Beispiel:

Wir nähern f(x):
 | (3.2) |
Dies folgt mittels der Rodrigues-Funktion. Etwas zur Notation:
Somit erhält man eine Näherung von f(x):
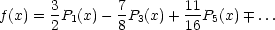
3.3.5 Randwertprobleme mit azimuthaler Symmetrie
Wir schreiben die Lösung
der Laplace-Gleichung in der Form:
![sum oo [ ]
f(r,h) = Alrl + Blr-(l+1) Pl(cosh)
l=0](th466x.gif)
Al und Bl folgen aus den Randwerten.
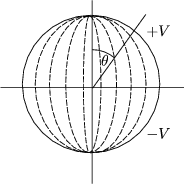
Beispiel:
 (r = a,
(r = a,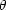 ) = V (
) = V (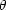 ) sei gegeben. Gesucht sei
) sei gegeben. Gesucht sei  im Inneren der Kugel. Im
Innern befindet sich keine Ladung. Daraus folgt, daß
im Inneren der Kugel. Im
Innern befindet sich keine Ladung. Daraus folgt, daß  im Inneren regulär
ist.
im Inneren regulär
ist.
Ich weiß also, daß das Potential im Innern keine Singularität aufweist. Bl muß
infolgedessen 0 sein. Al erhält man dadurch, daß man V nach Legendre-Funktionen
entwickelt:

Wir erhalten somit als Beispiel:



![[ ( ) ( ) ( ) ]
f(r,h) = V 3 r- P1(cosh)- 7 r-3P3(cosh)+ 11 r-5 P5(cosh)± ...
2 a 8 a 16 a](th473x.gif)
Ein analoges Problem ergibt sich für den Außenraum:
Aus dieser Bedingung geht hervor, daß die Koeffizienten Al 0 sein müssen, da
rl im Unendlichen nicht gegen 0, sondern gegen unendlich geht. Für Bl
folgt:
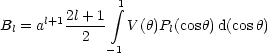
![[3(a )2 7(a )4 ]
f = V 2 r- P1 - 8 r- P3 ± ...](th476x.gif)
Aus der Beziehung geht hervor, daß es für große l einen starken Abfall
gibt.
Kugelflächenfunktion : m /= 0:
Die verallgemeinerte Legendre-Gleichung lautet, wie wir schon gesehen haben:
![|-------------------[--------------]----------|
|@-- 2 -@- m -m2--- m |
|@x(1- x )@x Pl (x)+ l(l+ 1)- 1- x2 Pl (x) = 0|
-----------------------------------------------](th479x.gif)
Dies hängt nur ab von m2. Wir behandeln den Fall m > 0, wobei bei x2 = 1 eine
Singularität liegt. Folgender Ansatz wird verwendet:

h(x) sei regulär bei x2 = 1. Wir untersuchen nun das Verhalten bei x2 = 1, wobei
wir zwei Terme haben:
- 1.Term:
![= -@-(1 - x2)-@-(1- x2)rh = -@-[(1- x2)r(1 - x2)r-1(-2x) +O((1 - x2)r+1)]h(x) =
@ |_ x @x @x _|
2 2 r- 1 2 2 r [ 2 2 r-1 2 r]
= |_ r (1- x ) 4x +O((1- x ) ) _| h(x) = 4r (1- x ) + O((1- x ) ) h(x)
~~ 4](th481x.gif) | (3.3) |
- 2.Term:
![[ 2 ]
l(l+ 1)- -m----(1- x2)rh(x) = - m2(1- x2)r-1h(x) + O((1- x2)r)
1- x2](th482x.gif)
Daraus folgt:
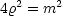
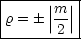
Wir setzen Plm = (1 - x2) h(x)m (*). Dies ergibt eine Differentialgleichung
für H mit regulären Koeffizienten. Man kann somit nach kurzer Rechnung
zeigen:
h(x)m (*). Dies ergibt eine Differentialgleichung
für H mit regulären Koeffizienten. Man kann somit nach kurzer Rechnung
zeigen:

Die Gleichung (*) ist somit erfüllt. Pl ist ein Polynom vom Grad l. Daraus
folgt:

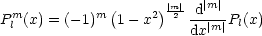
Es wird eine Normierung durchgeführt:
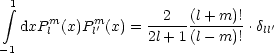
Die Kugelflächenfunktionen sind folgendermaßen definiert:
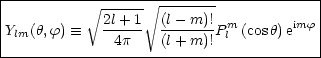
Dies ist auf der Kugeloberfläche das Analogon zur Fourierreihe. Des weiteren
gilt:

Beispiele:
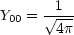
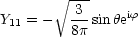


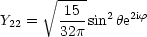
Jede Funktion auf der Kugeloberfläche kann folgendermaßen dargestellt
werden:
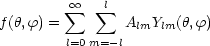
Jede Lösung der Laplace-Gleichung als:
![|------------------------------------|
| sum sum [ l - (l+1)] |
f = Almr + Blmr Ylm(h,f) |
-----l--m-----------------------------](th498x.gif)
Je nachdem, ob wir fordern, daß  regulär im Innern oder bei
regulär im Innern oder bei  ist, entfallen B
oder A.
ist, entfallen B
oder A.
3.3.6 Dipole und Multipol-Entwicklung
- Kartesische Koordinaten
- Darstellung in Polarkoordinaten:
Vorerst eine kleine Wiederholung dessen, was wir schon gelernt haben:
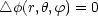

Wir führen eine Separation der Variablen durch:
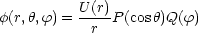
Mit x = cos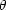 folgt und durch Multiplikation mit
folgt und durch Multiplikation mit 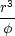 folgt:
folgt:

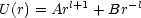
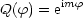

Plm sind die assoziierten Legendre-Polynome und Pl(x) die Legendre-Polynome.
Man führt an dieser Stelle die Kugelflächenfunktionen ein:
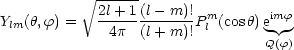
Das besondere an dieses Kugelflächenfunktionen ist nun, daß die ein
orthonormiertes Basissystem bilden:

Es sind also geeignete Funktionen für eine Entwicklung:


Daraus folgt die sehr wichtige Formel:

Die Kugelflächenfunktionen nähern Funktionen an, welche so ähnlich sind die
Kugelflächenfunktionen. Sie beschreiben also solche Systeme, die man sehr
gut durch Polarkoordinaten ausdrücke kann. Aber nun zurück zur
Multipolentwicklung:
Wir verwenden die Forderung, daß  (r
(r
 ) = 0 ist:
) = 0 ist:

Dies gilt außerhalb der Region mit Ladung. Es ist eine Entwicklung
nach abfallenden Potenzen in r. Des weiteren verwenden wir folgende
Gleichung:
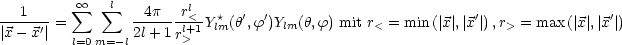
Diese wird in  (
(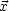 ) eingesetzt, wobei man die Multipolmomente erhält:
) eingesetzt, wobei man die Multipolmomente erhält:


Somit erhält man:
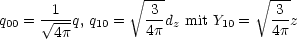

q2m ist linear in Qik (siehe Übung). Wir betrachten F' ||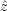 , also den
axialsymmetrischen Fall (m = 0):
, also den
axialsymmetrischen Fall (m = 0):

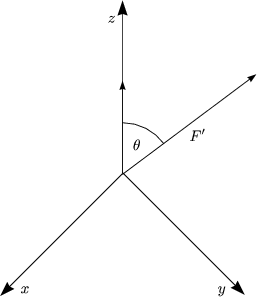
Wir bestimmen Al0, Bl0 für den Fall  ||
|| ' ||
' ||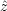 :
:
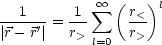
Wobei r> = max(r,r') und r< = min(r,r') ist. Damit folgt:

Den allgemeinen Fall erhält man mit Hilfe des Additions-Theorems für
sphärische Harmonische. Das Legendre-Polynom von cos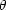 kann man
ausdrücken über eine Reihe von Kugelflächenfunktionen:
kann man
ausdrücken über eine Reihe von Kugelflächenfunktionen:

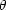 ist der Winkel zwischen r und r'. Dann ergibt sich:
ist der Winkel zwischen r und r'. Dann ergibt sich:
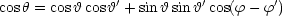




![]() =
= ![]() ist, muß
ist, muß ![]() im Außenraum senkrecht zur Fläche stehen.
im Außenraum senkrecht zur Fläche stehen.

![]() =const. im inneren Rand des Leiters. Falls sich
keine Ladungen im Inneren befinden, ist dies die einzige Lösung der
Laplace-Gleichung:
=const. im inneren Rand des Leiters. Falls sich
keine Ladungen im Inneren befinden, ist dies die einzige Lösung der
Laplace-Gleichung: ![]() ist somit konstant im Innern, womit gilt
ist somit konstant im Innern, womit gilt ![]() =
= ![]() . Dies
gilt im Innern auch bei Anwesenheit von Ladungen im Außenraum. Die
Ladungsträger richten sich so aus, daß sie das Feld im Innern abschirmen.
Dies ist also nichts anderes als ein Faradayscher Käfig. Zusammenfassend
kann man also sagen: Das Potential im Leiter ist konstant und das
elektrische Feld somit 0.
. Dies
gilt im Innern auch bei Anwesenheit von Ladungen im Außenraum. Die
Ladungsträger richten sich so aus, daß sie das Feld im Innern abschirmen.
Dies ist also nichts anderes als ein Faradayscher Käfig. Zusammenfassend
kann man also sagen: Das Potential im Leiter ist konstant und das
elektrische Feld somit 0.

![]() -Feldes steht senkrecht auf der Oberfläche. Die
Flächenladungsdichte
-Feldes steht senkrecht auf der Oberfläche. Die
Flächenladungsdichte ![]() ist:
ist:
![]() im Unendlichen gegen 0 ging.
Im folgenden werden aber Probleme behandelt, die Randbedingungen im
Endlichen, wie beispielsweise auf Flächen, aufweisen.
im Unendlichen gegen 0 ging.
Im folgenden werden aber Probleme behandelt, die Randbedingungen im
Endlichen, wie beispielsweise auf Flächen, aufweisen.


 bei x = 0 senkrecht auf der Ebene steht.
bei x = 0 senkrecht auf der Ebene steht.  muß
im Bereich x < 0 die Poisson-Gleichung erfüllen. Das Feld im Halbraum
x < 0 wird durch Ladung und Spiegelladung beschrieben. Mögliche
Fragestellungen sind daher:
muß
im Bereich x < 0 die Poisson-Gleichung erfüllen. Das Feld im Halbraum
x < 0 wird durch Ladung und Spiegelladung beschrieben. Mögliche
Fragestellungen sind daher:

![]() ’ im Innern der Kugel, so daß
’ im Innern der Kugel, so daß
![]() |
|![]() |=a = 0 ist. Wir verwenden den Ansatz (Ursprung im Mittelpunkt der
Kugel):
|=a = 0 ist. Wir verwenden den Ansatz (Ursprung im Mittelpunkt der
Kugel):
![]() ' = y'
' = y'![]() y. Außerdem fordern wir aufgrund der
Erdung:
y. Außerdem fordern wir aufgrund der
Erdung:
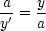
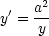
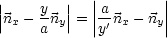
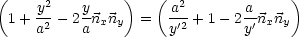

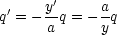

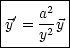
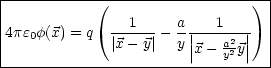
 = 0
auf der Kugeloberfläche. Was uns außerdem noch interessiert, ist das
elektrische Feld:
= 0
auf der Kugeloberfläche. Was uns außerdem noch interessiert, ist das
elektrische Feld:
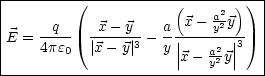
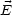 in radiale Richtung zeigen. Nach
Rechnung folgt:
in radiale Richtung zeigen. Nach
Rechnung folgt:
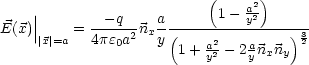
 | = a):
| = a):
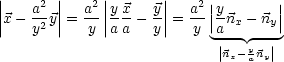
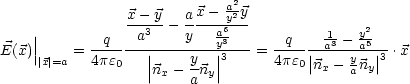


 q nimmt ab mit
wachsendem y und ist gleichmäßiger verteilt, wenn y größer wird.
q nimmt ab mit
wachsendem y und ist gleichmäßiger verteilt, wenn y größer wird.
 (
( ) liefert das von der Punktladung erzeugte Potential. Daraus folgt
dann die Greensche Funktion zur Randbedingung
) liefert das von der Punktladung erzeugte Potential. Daraus folgt
dann die Greensche Funktion zur Randbedingung  |
| |=a = 0.
Der Betrag der auf die Ladung q wirkenden Kraft ist:
|=a = 0.
Der Betrag der auf die Ladung q wirkenden Kraft ist:
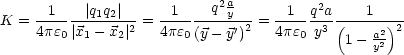

 q. Der Abstand zwischen Ladung
und Spiegelladung ist 2
q. Der Abstand zwischen Ladung
und Spiegelladung ist 2 . Für eine kontinuierliche Verteilung
. Für eine kontinuierliche Verteilung 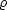 (
(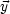 )
außerhalb der Kugel gilt:
)
außerhalb der Kugel gilt:
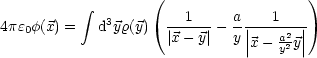
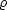 (
( ) ergibt sich das Potential zu:
) ergibt sich das Potential zu:
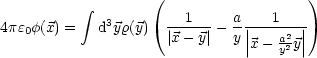

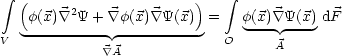


![|-----------------------------------------------------------------------|
| 1 integral ' ' ' 1 integral '[ ' ' ' '] |
|f(x) = 4pe0 dx G(x,x)r(x )- 4p- dF f(x ) \~/ x'G(x, x)- G(x,x ). \~/ x'f(x )|
------------V-------------------O---------------------------------------](th316x.gif)
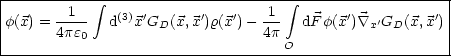
![( ) ( )
integral
d(3)x'' GD(x,x'') /_\ x''GD(x',x'') - / _\ x'GD(x,x'')GD(x',x'') =
V ----- ----- ----- -----
integral [( -4pd(x'-x'')) ( -4pd(x-x'') )]
= dF '' G (x,x'')-@--G(x',x'') - --@-G (x,x'').G (x',x'')
D @n'' @n'' D D
O](th338x.gif)


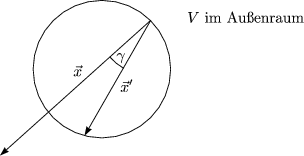

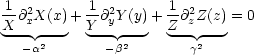

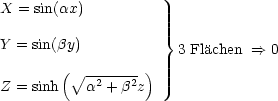
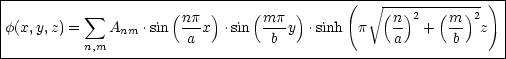



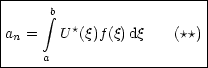
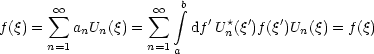

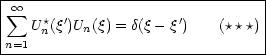
![|-------------------------------------------------|
| 1 sum oo [ (2pmx ) (2pmx )] |
|f(x) = 2 A0 + Am cos --a-- + Bm sin --a-- |
-------------m=1----------------------------------](th430x.gif)

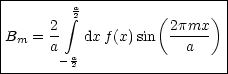
![2 2 [1 2 1 1 @ 2 @ ] 1 2
r (1- x ) U-@rU + r2P-@x-(1- x )@xP + Q-@fQ = 0
----------------- ----------------- ----
h¨angt nicht von f ab hv¨anognt r n,xic ahbt](th442x.gif)








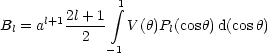
![= -@-(1 - x2)-@-(1- x2)rh = -@-[(1- x2)r(1 - x2)r-1(-2x) +O((1 - x2)r+1)]h(x) =
@ |_ x @x @x _|
2 2 r- 1 2 2 r [ 2 2 r-1 2 r]
= |_ r (1- x ) 4x +O((1- x ) ) _| h(x) = 4r (1- x ) + O((1- x ) ) h(x)
~~ 4](th481x.gif)