Kapitel 3
Elektrisches Feld, Ladungsdichte, Potential

• Gaußscher Satz in der Elektrostatik

  Durch das Coulomb-Gesetz läßt sich von der Ladung auf die Kraft schließen:

  

  Wir verallgemeinern auf die Ladungsdichte:

  

  Das Problem läßt sich auch umkehren, indem man aus dem vorgegebenen berechnen muß. Zunächst sei auf geschlossener Fläche gegeben, wobei sich im Ursprung eine Punktladung befinden sollte:

  

  

  
  

  

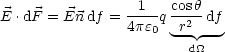
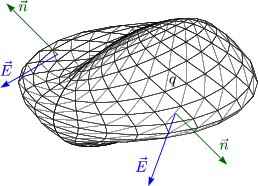
  Wegen der Additivität des Feldes gilt für mehrere Punktladungen:

  

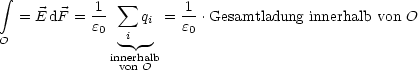
  Wir gehen nun zur Ladungsdichte über:

  

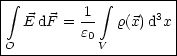
  V ist hierbei das von O eingeschlossene Volumen. Diese Beziehung nennt man auch Gaußsches Gesetz der Elektrostatik in Integralform. Wir verwenden nun:

  
  

  Daraus erhalten wir nun die differentielle Form des Gaußschen Gesetzes:

  

• Potential

  Aus () = _³d³x'(') ^. und -_x = folgt:

  

  Der Vorteil des Potentials ist, daß es sich um eine skalare Größe handelt. Es handelt sich somit um eine Funktion, statt der drei Komponenten von (). Wie kann man interpretieren?
  Stellen wir uns vor, eine Testladung q wird von ₁ nach ₂ transportiert, wobei die Kraft q ^.() auf q wirkt. Die aufzuwendende Arbeit berechnet sich nach:

  

  

  Es gilt:

  

  Diese Beziehung kann durch Nachrechnen gezeigt werden. Das Linienintegral über einem geschlossenen Weg erhält man mittels des Stokesschen Satzes:

  

  Durch Transport auf geschlossenem Weg kann aus wirbelfreiem Feld keine Energie gewonnen werden. Die zwei Grundgleichungen der Elektrostatik lauten nun:

  × =

  =

• Poisson- und Laplace-Gleichung

  Aus = und = - folgt nun:

  

  Dies ist die sogenannte Poisson-Gleichung. In Gebieten ohne Ladung läßt sich diese Gleichung folgendermaßen umformen:

  

  Hierbei handelt es sich um die Laplace-Gleichung, wobei der Laplace-Operator folgendermaßen definiert ist:

  

  Wir verifizieren die Poisson-Gleichung nun unter Verwendung von:

  

  Wir berechnen also:

  

  Nun wird eine Nebenrechnung durchgeführt, wobei bewiesen wird:

  

  Für ||0 gilt in Kugelkoordinaten:

  

  Am Ursprung ist ² zunächst nicht definiert. Für beliebig kleine V gilt mit dem Gaußschen Satz:

  

  Für eine Kugeloberfläche O mit Radius |₀| gilt:

  
  
  
  
  

  Also folgt:

  

• Energie des statischen Feldes
  Die Wechselwirkungsenergie eines Systems von Punktladungen lautet:
  
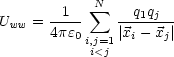
   3.1 Energie des statischen Feldes
   3.2 Oberflächenladungen
   3.3 Randwertprobleme in der Elektrostatik
    3.3.1 Green’sche Funktionen und ihre Anwendungen
    3.3.2 Laplace-Gleichung mit Randwerten auf Quader/Separation der Variablen
    3.3.3 Mathematischer Einschub:Orthogonale Funktionen, Entwicklungen, Fourier-Reihen
    3.3.4 Laplace-Gleichung in Kugelkoordinaten
    3.3.5 Randwertprobleme mit azimuthaler Symmetrie
    3.3.6 Dipole und Multipol-Entwicklung

  Beispiel:

  
  

  Wenn wir zusätzlich eine Ladung q₃ ins System bringen, gilt:

  
  

  Wir gehen nun zum Kontinuum über:

  
  

  Mittels der Poisson-Gleichung eliminieren wir nun ():

  

  Durch partielle Integration erhält man, wobei die Randterme verschwinden, weil und im Unendlichen gegen 0 gehen.

  
  

  Angewendet auf unsere Formel, ergibt sich: