4.12 Spin-Resonanz

[next] [prev] [prev-tail] [tail] [up]

4.12 Spin-Resonanz

1.Weg: $( ) ( ) E1- E2- |Y(t)> = C1(t)exp -i h t | |^ z>+ C2(t)exp - ih t | |, z>$
Basiszustand, C₁(t) und C₂(t) beschreiben die zeitabhängige Störung. Wir haben 2 lineare, gekoppelte Differentialgleichungen 1.Ordnung.
2.Weg:
Stelle Gleichungen für _x(t) = <(t)|_x|(t)> etc. auf und löse diese OHNE |(t)>, d.h. C₁(t), C₂(t) zu benutzen.

Der Hamilton-Operator lautet:

^H = M^ .B = -m B .^s -m B cos(wt)^s B 0 z B 1 x

( ) a 2 2 |Y(t)> = b , |a| + |b| = 1

---sx(t)---- < [ ] > d-<Y(t)| ^sx|Y(t)> = Y(t)|i-H^, ^sx |Y(t) dt h

Wir werten zuvor den Kommutator aus:

i i i --[H^, ^sx] =-(-mBB0) [^sz,s^x]+ -(- mBB0cos(wt))[^sx,^sx] h h 2^sy h

Man erhält somit ein System aus Differentialgleichungen:

d- dtsx(t) = w0sy(t)

-dsy(t) = - w0sx(t)+ wR cos(wt)sz(t) dt

d dtsz(t) = - wR cos(wt)sy(t)

Man nennt den Ausdruck _R = 2_BB₁ die Rabi-Frequenz und ₀ die Bloch-Frequenz. Anstelle eines linear polarisierten Feldes || x lege der Experimentalphysiker ein Drehfeld an:

Bw = (B1 cos(wt),B1 sin(wt),0)

Damit erhalten wir:

d-s (t) = w s (t)+ w sin(wt).s (t) dt x 0 y R z

d dtsy(t) = - w0sx(t)+ wR cos(wt)sz(t)

d-sz(t) = wRsin(wt)sx(t)- wRcos(wt)sy(t) dt

Dieses können wir in Form eines Kreuzproduktes schreiben:

d- dts(t) = _O_(t) ×s(t)

_O_ = _O_0 + _O_1(t) mit _O_0 = (0,0,- w0) und _O_1 = (- wRcos(wt),wR sin(wt),0)

Durch (t) wird die momentane Drehachse beschrieben.

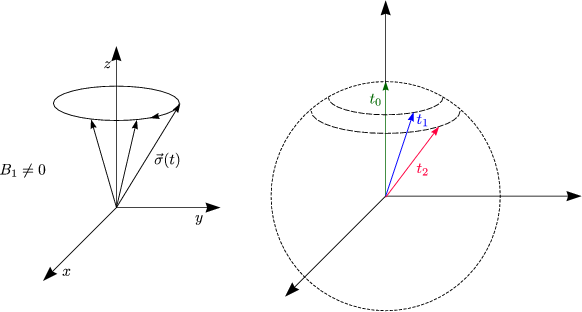
Wir haben eine Resonanz bei = ₀. Das „Umkippen“ des Spins nennt man Rabi-„Flopping“.

(1) |Y(t)> = |sz = 1> = 0

Dies ist stationär für B₁ = 0. Daraus folgt dann:

(a(t)) b(t)

Die Bewegung des Spin-Vektors setzt sich aus zwei Anteilen zusammen:

„Schnelle“ Bewegung um z (Larmor)
Langsame Bewegung (wenn _R « ₀) (Rabi-Oszillation)

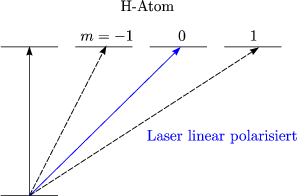
Es ergibt sich eine Aufspaltung durch „Pseudo-Magnetfeld“(beide Zustände $/\ =$ |>, |>).

Jedes nahezu resonant erregte System läßt sich als Zwei-Niveau-System beschreiben.
Jedes Zwei-Niveau-System ist äquivalent Spin im Magnetfeld

Ein rotierendes System (mit dem Drehfeld) wird beschrieben durch:

R1 = sx(t)cos(wt)- sy(t)sin(wt) R˙1 = -(w - w0)R2 } R2 = sxsin(wt)+ sy cos(wt) R˙2 = (w- w0)R1 + wRR3 R3 = sz(t) R˙3 = -wRR2

[next] [prev] [prev-tail] [front] [up]