Stationär=Klassische Physik, Reihe nach ![]()
Es gibt folgende Näherungsverfahren in der Quantenmechanik:
Stationär=Klassische Physik, Reihe nach ![]()
Die Störungsrechnung nach Schrödinger lautet:
![]()
![]() ist der Störoperator.
ist der Störoperator.
Die Störungsreihe lautet:
Die Korrekturen erster und zweiter Ordnung sind rekursiv.
Die Korrektur erster Ordnung ist also gerade durch den Erwartungswert von ![]()
![]() ,
also des Störoperators gegeben.
,
also des Störoperators gegeben.
Man nimmt als Basis die bekannten Wellenfunktionen ![]() n'(0). Die Energiekorrektur
zweiter Ordnung lautet:
n'(0). Die Energiekorrektur
zweiter Ordnung lautet:
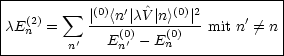
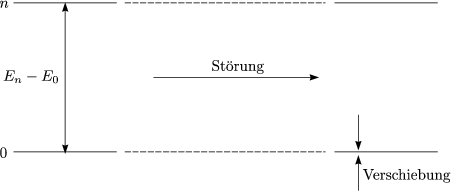
Das elektrische Potential für ![]() = (0,0,E0) lautet:
= (0,0,E0) lautet:
E0 sei hierbei der Stör-Parameter. Der Grundzustand wird beschrieben durch:

Für die Korrektur erster Ordnung gilt nun:
(Siehe auch Auswahlregeln für Dipolstrahlung) Wir berechnen die Korrektur 2.Ordnung:
Hier kommen sowohl die gebundenen als auch die Streuzustände vor. Beispielsweise berechnen wir <210|z|100>~ aB.
![i integral t [ Em - E0 -hw ]
C(1m)(t) = - h<m |V^|0>. exp i-----h------t' dt'
t0](th1059x.gif)
Der Anteil zu ![]()
![]() -
- ![]() ist nicht relevant. Mit t
ist nicht relevant. Mit t![]()
![]() ist |Cm(t)|2 ~ t.
ist |Cm(t)|2 ~ t.
An dieser Stelle wollen wir eine Rate definieren:
Man nennt diese auch Fermis Goldene Regel zur Berechnung der Übergangsintegrale. Die exakte Wellenfunktion lautet:
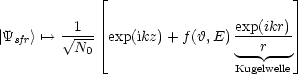
Es handelt sich hierbei (bis aus den Vorfaktor) um die Fourier-Transformierte von
V (r): ![]() (
(![]() ) mit dem Impuls-Übertrag
) mit dem Impuls-Übertrag ![]() =
= ![]() -
-![]() '
. Die Übergänge pro Sekunde
berechnen sich nach:
'
. Die Übergänge pro Sekunde
berechnen sich nach:
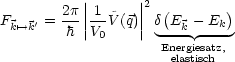
Die Summe der in d![]() gestreuten Teilchen ist dann:
gestreuten Teilchen ist dann:
Wir rechnen ein Beispiel mit der ![]() -Funktion:
-Funktion:
Mittels des elektrischen Dipolmoments ![]() = -e
= -e![]() erhalten wir dann:
erhalten wir dann:
![i< ||e || > integral t
C(m1)(t) = - h m |2 E0x|0 exp[i(wm - w)t']dt'
- oo](th1081x.gif)
Dei Störung wird adiabatisch eingeschaltet, um das Nicht-Abklingen der „homogenen Lösung“auszuschalten.
![integral t 1 ||t i
= i(w----w)+-d exp [i(wm - w)t]exp(dt)|| = (w-+-id)--w---exp[i(wm - w)t]exp(dt)
- oo m - oo ----- ---m-
Resonanz- Nenner](th1083x.gif)
d(t) ist reell:
![|------ sum -------------[--------------------------------------]-------------------|
|d(t) = |<m |e.x|0>| 2 .-------1---------+ ---------1-------- .q0 .exp(-iwt)exp(dt)
| m>1 Em -E0 - h(w+ id) Em - E0 + h(w +id) -------- --------|
| -------------------------- -------------------------- Komplexes angelegtes Feld
-----------------------Komplexe-Polarisierbarkeit d(w)------------------------------------](th1084x.gif)