[next] [prev] [prev-tail] [tail] [up]

8.4 Klassische relativistische Mechanik

Wir betrachten ein Teilchen der Masse m und Ladung e im elektromagnetischen Potential Am = (f,A). Wir setzen der Einfachheit halber h = c = 1. Die Teilchenbahn werde durch x(t) beschrieben. Außerdem führen wir den Vierervektor (xm) = (t,x(t)). Dann ergibt sich für dei Eigenzeit (Bogenlänge):

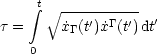
integral t V~ --------- t = ˙xG(t')˙xG(t')dt' 0

dt-= V~ ˙x-˙xm dt m

Dann ergibt sich durch Ableiten nach t:

d ˙xm = --xm = (1,v(t)) dt

dt = V~ 1---v2dt

Dann ergibt sich die Vierer-Geschwindigkeit durch Ableiten von xm nach der Zeit t:

m dxm(t) ---1--- dxm- u = dt = V~ 1---v2-dt

(um) = V~ -1---(1,v) 1 - v2

Der „kinematische Impuls“ bezeichnet man auch als „Vierervektor der Bewegungsgröße“:

m m --m---- TT := mu = (M, M v) mit der relativistischen Masse M = V~ 1---v2

[next] [prev] [prev-tail] [front] [up]