Hierbei handelt es sich um die relativistische Wellengleichung für ein Teilchen ohne Spin mit Masse m und Ladung e im elektromagnetischen Potential A. Die Schrödingergleichung „folgt“ aus der nichtrelativistischen Energie-Impuls-Beziehung:
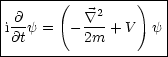
Relativistisch müssen wir die Transformation durchführen:
Die Wurzel ist leider problematisch. Wir verwenden deshalb die quadrierte Gleichung:
Daraus ergibt sich dann die KLEIN-GORDON-Gleichung:
![(--------)--------[----------------]-----|
| -@ 2 ( )2 2 |
| i@t - ef f(x) = -i \~/ - eA +m f(x) |
------------------------------------------](th523x.gif)
(x) = (t,
) ist im allgemeinen komplex.
![|----------------------------------|
[(i@m - eAm)(i@m - eAm)- m2]f(x) = 0 |
------------------------------------](th525x.gif){kind=small}
Mit der (eich-)kovarianten Ableitung D
:= D + ieA können wir die
KLEIN-GORDON-Gleichung außerdem schreiben als:
![|[----m----2]-----|
--DmD--+-m---f =-0|](th526x.gif){kind=small}
Falls A = 0 ist, gilt:
![(------2)-------|
-[]-+-m---f(x) =-0](th527x.gif){kind=small}