8.8 DIRAC-Gleichung (1928)

Die nichtrelativistische Pauli-Theorie des Elektrons (s = ) wird mit 2 Komponenten behandelt. Die relativistische Theorie benötigt den N-Komponenten-Spinor:

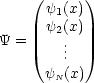
Betrachten wir nun den Produktraum E = E⁽⁰⁾ E^(s). Betrachten wir den Vektor |(t)> und eine Welle _s(x,t) <x,s|(t)>. Die Wahrscheinlichkeitsdichte ist dann gegeben durch:

Wir suchen nun eine Wellengleichung erster Ordnung:

H_D muß hierbei ein hermitescher Operator sein, weil diese nur dann die gleiche Struktur wie die Schrödingergleichung besitzt. Bei der Schrödingergleichung war eine komplexe Funktion; hier ist ein N-komponentiger Spinor. Das Relativitätsprinzip fordert eine gewisse Symmetrie zwischen Raum und Zeit. Da auf der linken Seite eine erste Ableitung nach t steht, muß in H_D deshalb auch eine erste Ableitung nach x erhalten sein. Wir machen deshalb den Ansatz:

_x, _y, _z und sind außerdem hermitesche Operatoren in E^(s). Üblicherweise können wir i E schreiben, womit also gilt:

1 ist eine Matrix im Spin-Raum, besteht aus drei Matrizen und m ist auch eine Matrix. Schreiben wir außerdem folgende Gleichung auf:

Die Idee ist, daß aus Gleichung (1) Gleichung (2) folgt, wenn ⁰ , + = 0 0 und ⁰⁰ = ¹¹ = ²² = ³³ = 1 gilt. Damit ist Gleichung (1) die wohlbekannte DIRAC-Gleichung. In dieser DIRAC-Gleichung befindet sich N-fach die KLEIN-GORDON-Gleichung.

Beweis:

m

Gilt ^kl + ^lk = 0, ^k + ^k = 0 und (^k)² = 1, ² = 1, so ergibt sich die DIRAC-Gleichung. Hierbei wird vorausgesetzt, daß es und gibt, welche diese Eigenschaften erfüllen. Dies ist der Fall für E^(s) > 4. Der übliche DIRAC-Spinor besitzt N = 4, was jedoch Zufall ist. Im elektromagnetischen Feld führen die Transformationen EE - e und - e durch, wobei e die Elementarladung ist.

Diese Form der DIRAC-Gleichung sieht nun aber gar nicht relativistisch aus. Deshalb wollen wir diese in kovarianter Form schreiben. Dazu multiplizieren wir von links mit :

Damit erhalten wir:

Von FEYNMAN stammt dann folgende Schreibweise:

Die genügen einer sogenannten CLIFFORD-Algebra:

Schreiben wir uns die sogenannten Hermitizitätsbedindungen auf:

Wir wollen dies überprüfen. Bekanntlich ist hermitesch; es gilt also ^† = . Des weiteren gilt mit den Antikommutatorbeziehungen zwischen ^m und :

Außerdem gilt = . Die -Matrizen haben nun die Dimension = 2, wobei D die Raumzeit-Dimension ist und [x] Entier(x) die Gaußsche Klammer (Treppenfunktion, „Jeder Zahl wird die größte ganze Zahl zugeordnet, welcher kleiner oder gleich der Zahl ist.“). Betrachten wir folgende Beispiele: Für D = 1 + 1 gilt N = 2, für D = 2 + 1 erhalten wir N = 2, für D = 3 + 1 entsprechend N = 4 und schließlich ergibt sich für D = 9 + 1, daß N = 32 ist. Schauen wir uns für D = 4 die DIRAC-Darstellung ________________ an:

^m sind hierbei die Pauli-Matrizen:

Zu Hause kann als Übung überprüft werden, ob diese tatsächlich die CLIFFORD-Algebra erfüllen. In dieser Darstellung wird die Energie diagonal sein, da diese mit = ⁰ verknüpft ist. Eine andere Darstellung ist die sogenannte MAJORANA-Darstellung ____________________:

Auch diese Darstellung genügt der CLIFFORD-Algebra. In dieser Darstellung ist die DIRAC-Gleichung reell; man kann daher die Lösungen (Spinoren) reell wählen.

Greifen wir nun im folgenden auf DIRAC-Spinoren zurück. Betrachten wir dazu den folgenden komplexen Spinor:

Also folgt daraus die adjungierte DIRAC-Gleichung:

Wir berechnen nun ^. (1) - (1) ^. :

Also gilt i = 0. Mit der Stromdichte j erhalten wir die Kontinuitätsgleichung j = 0.