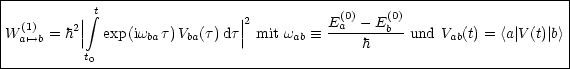Hier soll nun H(0) zeitunabhängig sein.
Das Eigenwertproblem von H(0) sei des weiteren gelöst; wir kennen also
Eigenvektoren |a> mit H(0)|a> = Ea(0)|a>. Definiere die BOHRsche Frequenz
![]() ab =
ab = ![]() (Ea(0) - Eb(0)) und das Übergangsmatrixelement V ab(t) = <a|V (t)|b>.
Das System befinde sich zur Zeit t0 im H(0)-Eigenzustand |a>. Wir suchen
die Wahrscheinlichkeit, das System zur Zeit t im H(0)-Eigenzustand |b> zu
finden:
(Ea(0) - Eb(0)) und das Übergangsmatrixelement V ab(t) = <a|V (t)|b>.
Das System befinde sich zur Zeit t0 im H(0)-Eigenzustand |a>. Wir suchen
die Wahrscheinlichkeit, das System zur Zeit t im H(0)-Eigenzustand |b> zu
finden:
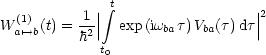
Wir lösen die Schrödingergleichung iterativ:
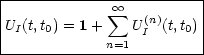
H(0) sei zeitunabhängig. Die Übergangswahrscheinlichkeit von Zustand a nach Zustand b ist gegeben durch: