[next] [prev] [prev-tail] [tail] [up]

10.2 FERMIs Goldene Regel

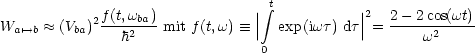
Es sei V = const. für t > 0 mit t0 = 0:

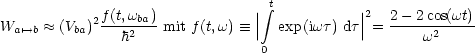
| integral t | Wa'-->b ~~ (Vba)2f(t,wba) mit f(t,w) =_ || exp(iwt) dt||2= 2--2-cos(wt) h2 w2 0

PIC

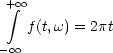
+ integral oo f(t,w) = 2pt - oo

Betrachten wir Übergänge in eine Gruppe B von Zuständen |b> mit benachbarter Energie Eb ± dE.

Lösung:
Es sei <b|b'> = ' d(bn-(bb)) mit n(b) (- R > 0.
integral integral P = |b>n(b)db<b|= |b>r (E)dE <b| B b B B(E)

varrhob(E) ist hierbei die Dichte der Niveaus b zur Energie E, also rb(E) =_ n(b)-db- dE. Dann ist die Wahrscheinlichkeit, vom Zustand a zu den Zuständen des Bereichs B zu gelangen, gegeben durch:

integral < † > Wa'-->B = a| U (t,0)PBPBU (t,0)| a = Wa'-->brb(E) dE mit PBPB = PB B(E)

Es sei E(b) = [ ] E1- e2,E1 + e2, t groß und e »2pht-:

integral Wa'-->B ~~ |Vab| 2rbf(t,wba)dE ~~ 2p-|Vba(Ea)|2rb(Ea)t h2 Annahme h

Damit erhalten wir FERMIs Goldene Regel:

|---------------------------| | dWa'-->B-- 2p- 2 | -wa'-->B- =_ ---dt--- ~~ -h-|Vba|-rb|

[next] [prev] [prev-tail] [front] [up]