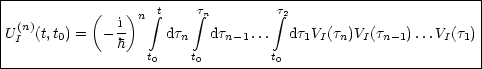Kapitel 10
Zeitabhängige Störungstheorie

und die Anfangsbedingung U(t₀,t₀ = 1. U(t,t₀) ist hierbei unitär und H(t) hermitesch. U hat außerdem die Eigenschaft U(t₂,t₀) = U(t₂,t₁) ^. U(t₁,t₀) für t₂ > t₁ > t₀. Man bezeichnet diese Beziehung auch als „Zusammensetzungsregel“. Falls H zeitunabhängig ist, gilt U(t,t₀) = exp.

Wir machen nun den Störungsansatz H(t) = H⁽⁰⁾(t) + V (t), wobei V (t) eine Störung sein soll. Wir setzen voraus, daß die ungestörte Gleichung iU⁽⁰⁾(t,t₀) = H⁽⁰⁾(t)U⁽⁰⁾(t,t₀) bereits gelöst ist und arbeiten im Wechselwirkungsbild:

• U_I(t,t₀) := U^(0)†(t,t₀)U(t,t₀)
• |(t)>_I = U_I(t,t₀)|(t₀)>_I mit |(t₀)>_I = |(t₀)>

  Aus diesen beiden Bedingungen ergibt sich dann:

  

• Für Operatoren A gilt:

Wir stellen die Schrödingergleichung für U_I auf:

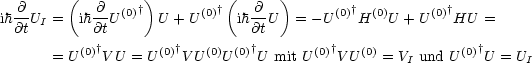(10.1)

Wir integrieren von t₀ nach t und erhalten eine Integralgleichung:

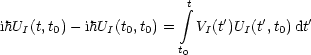
Mit U_I(t₀,t₀) = 1 erhalten wir:

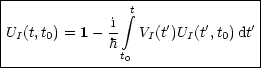
Diese Integralgleichung wollen wir durch Iteration lösen:

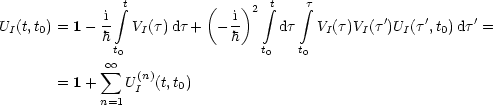(10.2)