6.2 Geschwindigkeitsgesetze und integrierte Geschwindigkeitsgleichungen

[next] [prev] [prev-tail] [tail] [up]

6.2 Geschwindigkeitsgesetze und integrierte Geschwindigkeitsgleichungen

Reaktion 0-ter Ordnung

$dnA- 0 - dt = k0nA = k0$

$- dn = k dt A 0$

$n (t) A integral integral - dnA = k0 dt nA(t=0)$

$-nA(t')+ nA(t = 0) = k0t'$

$' ' nA(t) = nA(t = 0)- k0t$
Reaktion erster Ordnung A k₁ B

$d[A] ----- = k1[A]1 dt$
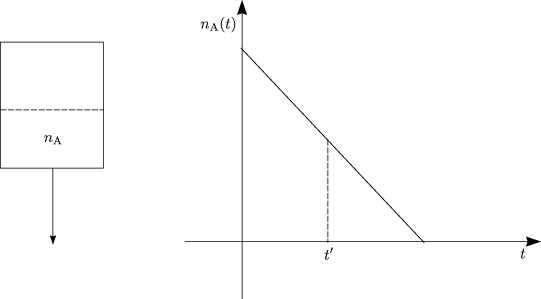
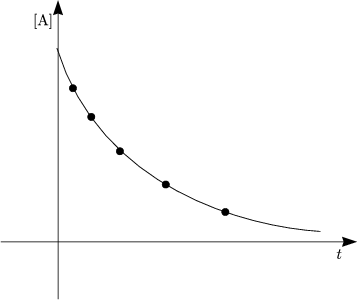
Dies ist eine Differentialgleichung 1.Ordnung, die wir durch Trennung der Veränderlichen lösen:
$d[A]= k1 dt [A]$
Nun werden beide Seiten integriert und wir erhalten:
$[A integral ] integral t d[A] = -k1 dt [A] t=0 [A]0$
Indem wir jetzt beide Seiten exponieren und nach [A] auflösen, erhalten wir:
$( ) -[A]- ln [A]0 = -k1t$

$[A(t)] = [A]0exp(- k1t)$

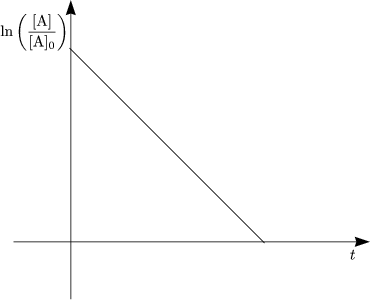
Die Dimension von k₁ ist . Wir erhalten dann für die Halbwertszeit t_1/2:
$( ) 1 = exp -kt1/2 2$

$|--------------------| | 1- 0,693 | t1/2 = k1(ln 2) ~~ k1 | ----------------------$
Die mittlere Lebensdauer ist [A] = [A]e^-1 = [A]exp.

$d[A]= - d[B]= - k1[A] dt dt$

$[A]t = [A] (- k1t) = [A] - [B]$
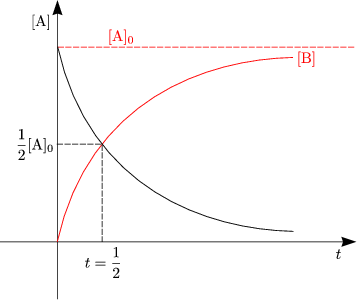
Wir nehmen an, daß [B]₀ = 0 gilt.
$[B] = [A] (1- (-k t)) = [B] (1 -(- k t)) 0 1 0 1$
Reaktion erster Ordnung mit Rückreaktion erster Ordnung A₂]k₁ B
Ein Beispiel hierfür ist die Isomerisierung. k_A und k_B sind Reaktionsgeschwindigkeitskonstanten erster Ordnung.
$[A]- d[B] - dt = kA[A]- kB[B]; dt = kA[A]- kB[B]$
Via Massenerhalt
$d([A] + [B] ----dt----= 0 <==> [A] + [B] = const.$
läßt sich diese Differentialgleichung noch vereinfachen:
$[A]+ [B] = [A]0 + [B]0 = [A] oo + [B] oo$

$[B] = [A] + [B] - [A] 0 0$

$d[A] = -k [A]+ k [A] + k [B] - k [A] dt A B 0 B 0 B$

$d[A] [ kB ] -dt- = -k(kA +kB) [A] - (kA +-kB)-([A]0 + [B]0)$
Es gilt:
$d([A]--const.)-= d[A] dt dt$

$d([A]---const.) dt = - (kA + kB)([A] - const.)$

$dx- dt = - (kA + kB)x$
Nach Integration folgt lnx = -(k_A + k_B)t + C.
$x = C exp(- (k + k )t) A B$

$[A]- --kB---([A]0 + [B]0) = C exp(-(kA + kB)t) kA + kB$
Einsetzen von t = 0 ergibt:
$C = [A] - ---kB--([A] + [B] ) 0 kA + kB 0 0$

$( ) --kB--- ---kB--- [A(t)] = [A]0 - kA + kB ([A]0 + [B]0) exp (- (kA + kB)t)+kA + kB ([A]+ [B]0)$

$[A]- [A] oo = [B] oo - [B]$
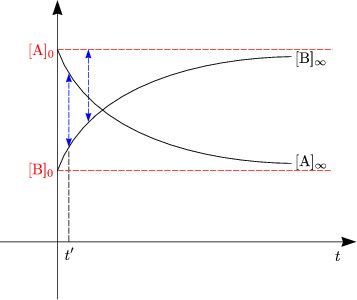
Daraus ergibt sich:
$([A]0- [A] oo ) exp(- (kB + kA)t) = = ([B] oo - [B0])exp(- (kB + kA)t)$ (6.1)
Bei t = gilt: $d[A] [B] [B] oo ---- = - ---= 0 und K = ----- dt dt [A] oo$

$d[A] dt = -kA[A]+ kB[B] ==> kA[A] oo = kB[B] oo$
Reaktion zweiter Ordnung in A - keine Rückreaktion
Betrachten wir die Reaktion:
$2A --> P(A + B --> P)$

$( ) - 1 d[A] = k2[A]2 2 dt$

$integral [A] integral t d[A] = -2k dt [A]2 2 [A]0 0$

$( ) --1-- -1-- - [A(t)]- [A]0 = -2k2t$

$1 1 [A(t)] = [A]-+ 2k2t 0$

$|-----------------------------| |---1---- -1--1 -1-- | |[A(t1/2)] = [A]0 2 = [A]0 + 2kt1/2| -------------------------------$
Damit erhalten wir folgende Halbwertszeit:
$t1/2 = --1---- 2k2[A]0$
Es handelt es um eine Reaktion 2.Ordnung. Die Halbwertszeit ist abhängig von der Anfangskonzentration. Eine manchmal nützliche Darstellung ist:
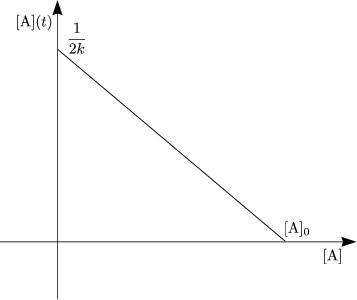Diese Darstellung basiert auf:
$1--- -1-= 2kt [A] [B]$
Wir multiplizieren mit und erhalten:
$|-----------------| |-1-- -[A]--= [A]t| -2k---2k[A]0-------|$
Reaktionen mit Gesamtordnung 2: erster Ordnung in A B $k2 A + B ---> C$

$d[A] d[B] d[C] -dt-= - k2[A][B] = -dt-= - -dt-$

$integral x dx integral t ([A]---x)([B]---x)-= k2 dt 0 0 0 0$
Zur Integration müssen wir eine Partialbruchzerlegung durchführen:
$1 ( ([A] - x ) ([B] -x )) ----------- ln --0---- - ln --0---- = k2t ([B]0- [A]0) [A]0 [B]0$

$|-----------------------------| ( 1 ) ([B]0[A]0) | | [B]---[A]- ln -[A]-[B] = k2t| ----0-----0--------0-----------$
Diese Gleichung gilt jedoch nicht für [A]₀ = [B]₀. Wenn [B]₀ » [A]₀ und x « [B]₀ ist, ist folgende Näherung nützlich:
$( ) [B] - ~ [B]0-- > [A] - ~ [A]0exp -k2[B]0 t --'-- k2$
Es handelt sich also um eine Kinetik pseudo-erster Ordnung.

[next] [prev] [prev-tail] [front] [up]