2.5 Heisenbergsche Unschärferelation

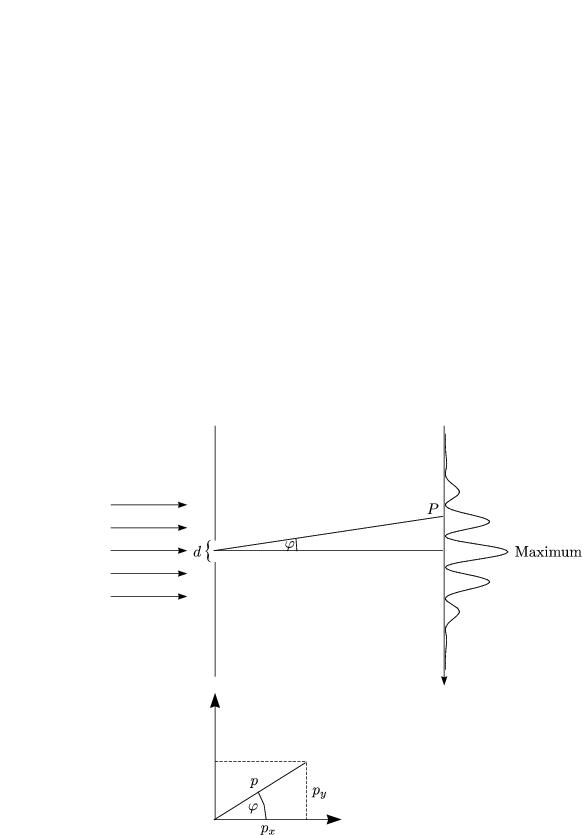
Wir betrachten die Messung der x-Koordinate und der x-Komponente des Impulses eines mikroskopischen Teilchens.

Beispiel: Elektronenbeugung am Spalt

Zu Beginn liegt eine Teilchendichte vor, welche durch die Wellenfunktion beschrieben wird. Hierbei tritt nur die y-Komponente und keine x-Komponenten auf. Nach Spalt der Breite d liegt dann die Unsicherheit x d für die x-Komponente und die Unsicherheit p_x = psin für die p_x-Komponente vor. Am Spalt gilt dann x ^. p_x = dpsin. Aus der Beugungstheorie ergibt sich sin = . Dies wird eingesetzt und man erhält:

Mit der de Broglie-Beziehung p = k = mit k = , wobei k der Wellenvektor ist, ergibt sich = und damit xp_x h. Die exakte Formulierung ist folgende:

Rechenregeln:

• = -
• = = k

Beispielsweise gilt:

Die Zustandsfunktion kann nicht gleichzeitig Eigenfunktion von und _x sein. Eine gleichzeitige Angabe exakter Werte für x und p_x ist nicht möglich. Für eine Zustandsfunktion , die keine Eigenfunktion von  ist, bekommt man mehrere Werte für A in identischen Systemen. Die Standardabweichung ist gegeben durch:

Beispiel:

In Worten:

2.5.1 „Energie-Zeit“-Unschärferelation

Strenggenommen gibt es keinen Zeitoperator in der Quantenmechanik. Energie und Zeit sind folglich keine Kommutatoren. Stattdessen betrachten wir jetzt Energie- und Zeitunschärfe als Aspekt der zeitabhängigen Schrödingergleichung und definieren uns eine sogenannte Lebensdauerverbreiterung:

Jedem Zustand mit einer endlichen Lebensdauer kann nur eine unscharfe Energie zugeordnet werden. Wenn man das konsequent macht, erhält man E , wobei die Zeitkonstante für den Abfall (der Lebensdauer eines Zustandes) ist. Diese Zeit-Energieunschärfe ist Grundlage in der Spektroskopie.

Beispiel: Femtosekundenlaser

Es sei _p = 30fs = 3 ^. 10^-14 s. Beispielsweise gilt für ein Gauß-förmiges Strahlprofil _p ^. E = 0,441. Daraus ergibt sich:

Das heißt, es gilt _max = 800nm und = 31nm.