2.6 Einfache Anwendungen der Quantenmechanik

2.6.1 Teilchen im Kasten

Beispiel:

• Konjugierte Kohlenwasserstoffatome (Butadien)
  • Farbstoffe, Polymere
• Erweiterung auf Elektronen im Metall (periodisches Potential)

Vorgehen:

1. Gesamtenergie klassisch aufschreiben
2. Übersetzung in Operatoren
3. Lösung der Schrödinger-Gleichung (Differentialgleichung) suchen, die stetig, eindeutig und endlich ist

2.6.2 Lösung der Schrödinger-Gleichung für die Translationsbewegung eines Teilchens mit Masse m im eindimensionalen Kasten

Teilchen im Kasten: Schrödinger-Gleichung für Teilchen im Potential

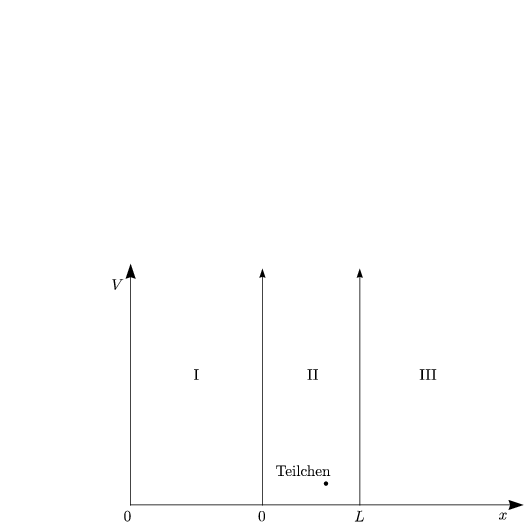
Das Teilchen kann klassisch jede beliebige Energie annehmen.

• H = + V , V = 0 für 0 < x < L und V = für x < 0 x > L
• = _const. + _const. = 0

  Dies ist eine Differentialgleichung 2.Ordnung.

• Lösung der Schrödingergleichung:

  Außerhalb des Kastens ist nur = 0 möglich, da V gilt. Die Lösung innerhalb des Kastens ist = Asinkx+B coskx. Aufgrund der Stetigkeit für x = 0 und x = L ergeben sich die Bedingungen (0) = (L) = 0. Hieraus ergibt sich dann B = 0 und sinkx = 0. Mit kL = n sind nur diskrete Lösungen möglich mit n = 1, 2, 3, ..., .

  

Endlichkeit, d.h. Normierung, Aufenthaltswahrscheinlichkeit:

Siehe beispielsweise BRONSTEIN:

Es ergibt sich hieraus A = und damit können wir die Eigenfunktionen für Teilchen im eindimensionalen Kasten aufschreiben:

Die Lösungen sind stehende Wellen. Des weiteren berechnen wir die Eigenwerte der Energie:

Dies kann bewerkstelligt werden durch Einsetzen von

in die Schrödingergleichung. Dazu bilden wir die 1. und 2. Ableitung:

Daraus erhalten wir schlußendlich:

Es liegen nur diskrete Energiewerte vor (Quantelung).

2.6.3 Diskussion der Eigenfunktion (x), der Aufenthaltswahrscheinlichkeit |(x)|² und der Energieeigenwerte E_n

Unschärferelation:

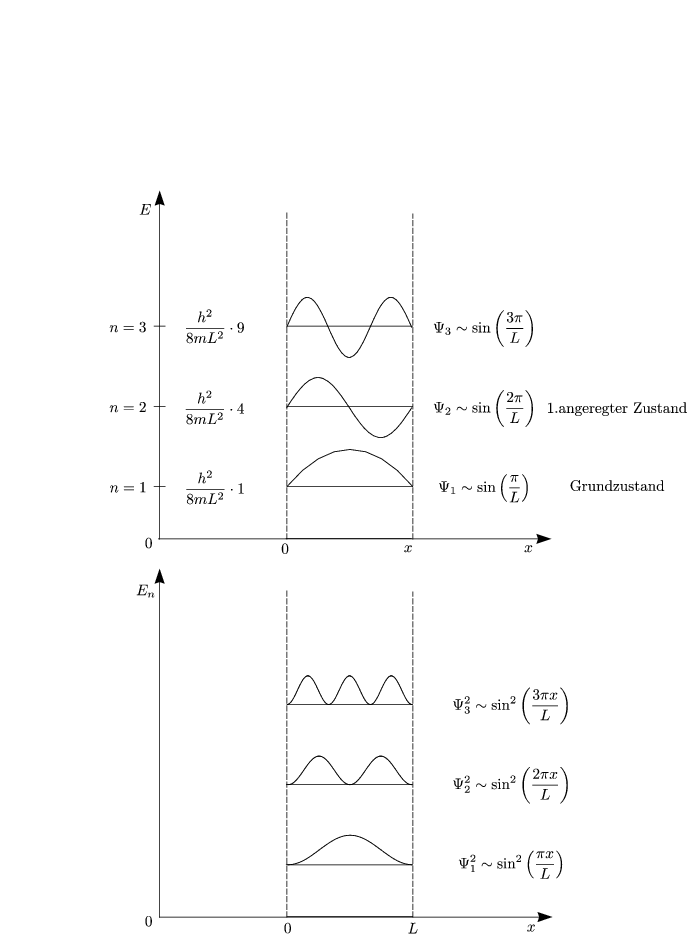
Wenn wir den Kasten größer machen (L größer), dann wird x größer, die Position wird unschärfer. Wenn p_x kleiner wird, kann man den Impuls exakter angeben. Die „Nullpunktsenergie“ ist:

Wichtige Merkmale:

1. Korrespondenzprinzip: Klassische Aufenthaltswahrscheinlichkeit für Teilchen im Kasten überall gleich groß. Das Verhalten wird angenähert für große n.

   

   Die klassische Mechanik ist ein Grenzfall der Quantenmechanik für n.

2. Energiezustände immer dichter für n

   Es liegt dann ein kontinuierliches Energiespektrum vor.

   

3. <p_x> = 0: Teilchen fliegen gleichwahrscheinlich nach links und rechts (stationärer Zustand)
4. Anwendung, beispielsweise Cyanin-Farbstoff Absorptionsspektrum
   

2.6.4 Der Tunneleffekt

Beispiel: Elektron-Transfer-Reaktionen:

Der Tunneleffekt ist im allgemeinen wichtig bei Teilchen mit kleiner Masse (Elektronen, Protonen, Neutronen)

Rastertunnelmikroskopie (STM):

Behandlung wie Teilchen im eindimensionalen Kasten, aber mit endlicher Höhe und Dicke der „Wände“ (Potentialwände/Barrieren).

1. Ankommende und reflektierte Wellen
2. Exponentieller Abfall
3. Veränderte Amplitude

2.6.5 Lösung der Schrödinger-Gleichung für Teilchen im zweidimensionalen Kasten

Anwendung:

„Quantengehege“ (quantum corral): EIGLER (IBM)

Fe auf Cu(111)

• Rechteck
• Stadion (Oval)

2.6.6 Lösung der Schrödinger-Gleichung für Teilchen im dreidimensionalen Kasten

Es gilt V (x,y,z) = 0 innerhalb des Kastens und V außerhalb. Die Schrödinger-Gleichung für dreidimensionalen Fall lautet:

Als Lösungsansatz führen wir eine Trennung der Variablen durch: (x,y,z) = X(x)Y (y)Z(z). Man erhält damit 3 Differentialgleichungen:

Für die Energieeigenwerte gilt:

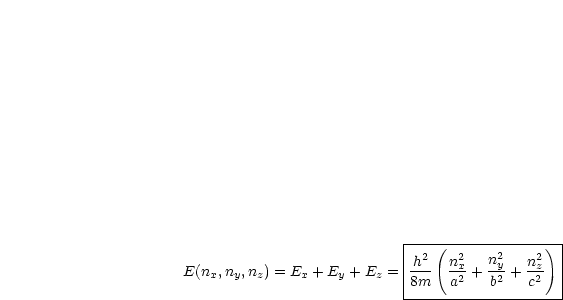
3-fache Entartung liegt vor, wenn gilt:

Ein allgemeines Prinzip der Quantenmechanik ist, daß die Entartung als Resultat der zugrundeliegenden Symmetrie aufgehoben wird.

Beispiel für Anwendungen des Teilchens im 3d-Kasten:

In der statistischen Thermodynamik läßt sich die molekulare Zustandssumme

beispielsweise angegeben durch