2.7 Der harmonische Oszillator

Teilchen im Kasten:

Molekülbindungen können beispielsweise gut durch das Morse-Potential beschrieben werden:

|------------------------| | ( - b(x-x0))2 | |V(x) = De 1 - e | -------------------------

D_e ist hierbei die Dissoziationsenergie und eine molekülspezifische Konstante. Wir entwickeln das ganze in eine Taylor-Reihe:

2 || V(x) ~~ V (x0) + 0+ 1 @-V2|| Dx2 2 @x- x=x0 Kraftkonstante k

Man bezeichnet diese auch als harmonische Näherung.

Vorschrift für Berechnung des harmonischen Oszillators:

Gesamtenergie $2 H = p--+ V mit V = 1kx2 2m 2$
Übersetzen in Operatoren $^ h2-@2-- 1 2 H = - 2m @x2 + 2kx$
Lösen der Schrödingergleichung $|----------------------------------------------------| | h2@2Y 1 2 @2Y (2mE mkx2) | |-2m--@x2 + 2kx Y = EY <==> @x2-+ -h2-- -h2-- Y = 0 | -----------------------------------------------------$
Diese ist eine Differentialgleichung vom Typ:
$V~ ---- @2Y- ( 2 2) 2mE-- km- @x2 + e- a x Y = 0 mit e = h2 und a = h$
Dazu verwenden wir folgenden Lösungsansatz:
$-a2x2 f(x) = e 2 .Y(x)$
Die allgemeine Lösung sind Eigenfunktionen _n der Form:
$|-------------------------| | ( 1 ) ( 2x2) | Yn(x) = N .Polynom .Gau ß-Funktion =|Nn .Hn a2x exp - a 2 | ---------------------------$
n ist hierbei eine Quantenzahl. Die charakteristische Frequenz (Schwingungsfrequenz) ist gegeben durch:
$|---------------------------------------------------------| | V~ --- V~ -- | n =-w-= |-1- k-bzw. n = 1-- k-mit der reduzierten Masse m =-m1-.m2- | 2p -2p---m----------2p--m---------------------------m1-+-m2--|$
Für die Normierungskonstante N_n gilt außerdem:
$|----------------------| | V~ --1--- ( V~ a-)14| |Nn = 2n .n!-. p- | -----------------------$
H_n(x) sind die sogenannten Hermiteschen Polynome:
$|------------------------------------| | 2 n - q2n- | |Hn(q) = (- 1)neq .d-e-n-mit q = a 12 .x -------------------dq----------------$

$H0 = 1, H1 = 2q, H2 = 4q2 -2, H3 = 8q3 - 12q$
Hermitesche Polynome gehorchen außerdem der Rekursionsbeziehung:
$|----------------------------| |qHn(q) = nHn -1(q)+ 1Hn+1(q)| --------------------2--------|$
Zu jedem _n gehört ein Energieeigenwert E_n:
$|-----------------------------| | ( 1)' ( 1) | |En = hw n + - = hn n + - | --------------2------------2--$

2.7.1 Eigenschaften des harmonischen Oszillators

Energiezustände:
Wellenfunktion:

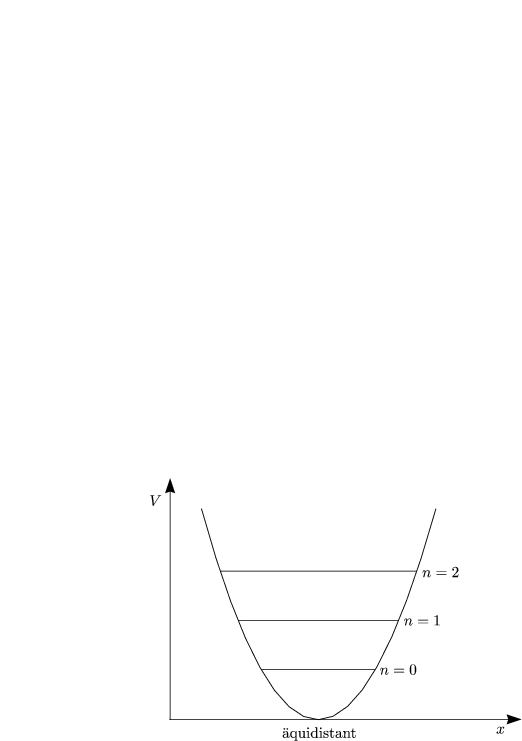
Die Nullpunktsenergie beträgt E₀ = h und die Zahl der Knoten ist gleich n.
Aufenthaltswahrscheinlichkeit:

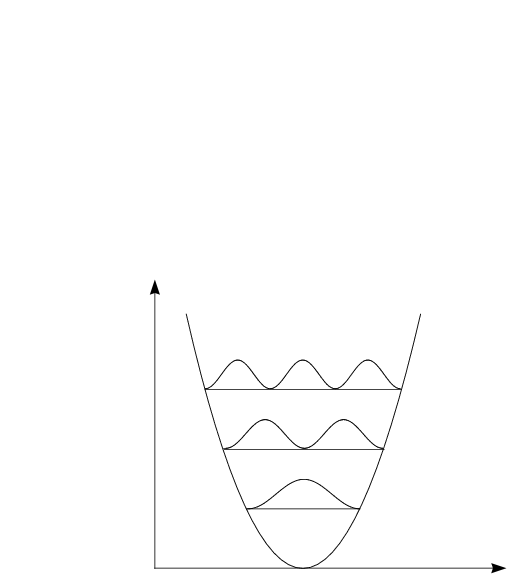
Die Aufenthaltswahrscheinlichkeit ist ². Für n gilt das Korrespondenzprinzip. Das größte ² findet sich in der Nähe der Umkehrpunkte (analog zur klassischen Mechanik). Das Nullpunktsniveau weicht jedoch von der klassischen Mechanik ab.

[next] [prev] [prev-tail] [front] [up]