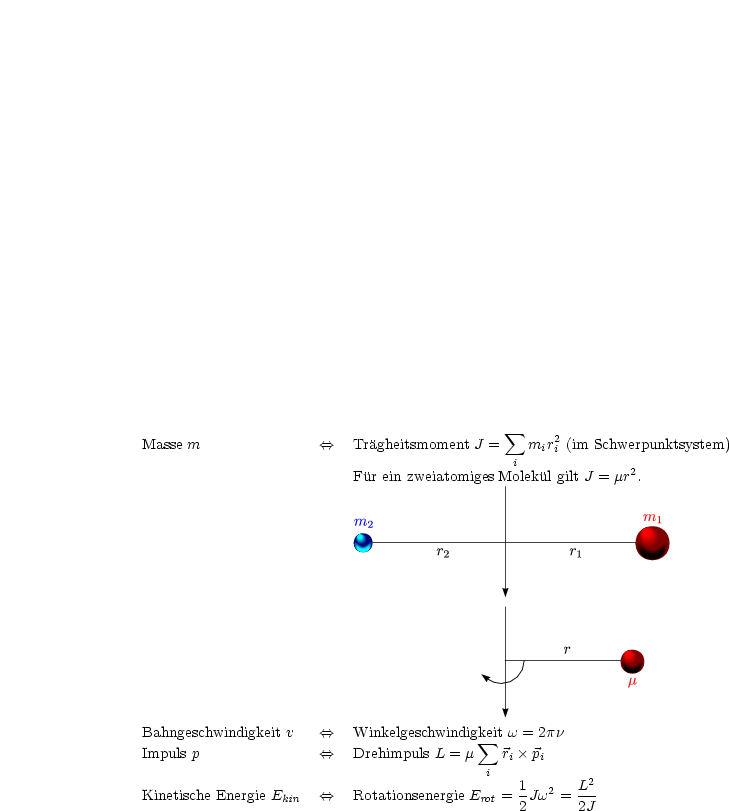
Wir nehmen an, daß der Rotator starr sei, das heißt, Schwingungen seien vernachlässigbar klein. Die Gesamtenergie besteht damit nur aus kinetischer Energie; es gibt keine potentielle Energie.
Wir wandeln das ganze von kartesischen Koordinaten in Polarkoordinaten um. Der Abstand vom Schwerpunkt ist somit konstant und die Richtungen werden durch zwei Winkel festgelegt.
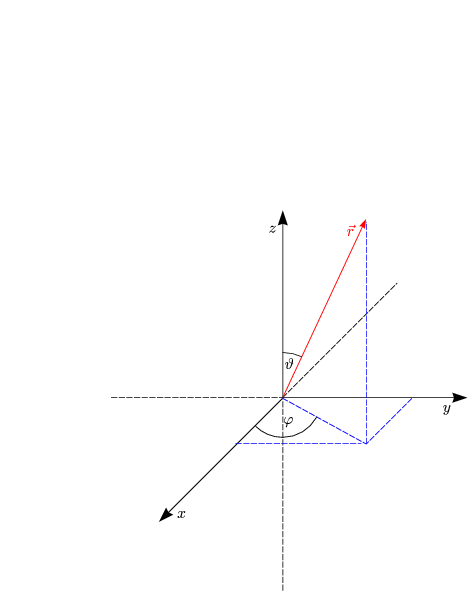
Für den Hamiltonoperator gilt dann:
Für einen starren Rotator ist r = const. = r0. Wir stellen die Schrödingergleichung auf:
![[ ( ) ]
-h2- --1--@- @Y- --1-- @2Y-
==> - 2mr20 sinh@h sinh @h + sin2h @f2 = EY](ch212x.gif){kind=small}
Wir machen einen Lösungsansatz in der Form Trennung der Variablen:
= 
(
),
(
). Einsetzen und Umformen ergibt:
und sind unabhängige Variablen.
Beide Seiten müssen konstant = m2 sein. Wir erhalten zwei neue Differentialgleichungen:
+ m2 = 0
Deren Lösung lautet = exp(im) mit m = 0, ±1, ±2, ....
+ 
= m2 mit -1 < x < 1 
0 < < 
Diese Differentialgleichung ist von folgender Form:
Die Lösungen dieser Gleichung für m = 0, ±1, ±2, ..., ±l sind die
assoziierten Legendre-Polynome 
() = Pem(cos).
Damit ergeben sich folgende Eigenfunktionen (,):
Betrachten wir als Beispiel explizite Lösungen für :
Wichtige Eigenschaften sind die beiden Quantenzahlen ml und l:
Man bezeichnet l als Drehimpulsquantenzahl. Mit l ist auch die Rotationsenergie gequantelt:
