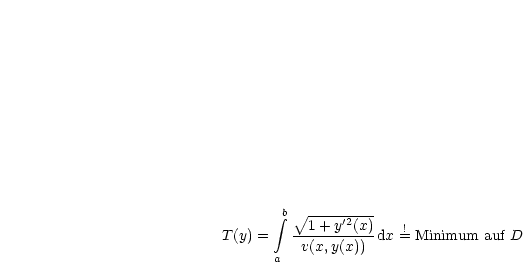[next] [prev] [prev-tail] [tail] [up]

1.3 „Fermatsches Prinzip“

Gegeben sei ein Medium G (_ R3 mit (x,y,z) (- G und der Geschwindigkeit des Lichts v = v(x,y,z) an dieser Stelle. A, B (- G seien Punkte. Gesucht ist der Weg des Lichtes in G von A nach B. Das Fermatsche Prinzip besagt nun:

|----------------------------------------------------------------------------------------| | | |Das Licht wa¨hlt den Weg, den es in k¨urzester Zeit zur¨ucklegen kann. | -----------------------------------------------------------------------------------------

PIC

r(t0) = rA, r(t1) = rB

Die Zeit von A nach B auf der Kurve r = r(t) ist nun:

integral B ds T (r) = v- A

Die mathematische Formulierung lautet folgendermaßen:

{ ( )3 } D = r = r(t) (- ^C1[t0,t1] , r(t0) = rA, r(t1) = rB

Gesucht ist nun r = rmin(t) (- D mit T(rmin) < T(r) A r (- D, wobei gilt:

integral ||r'(t)|| T(r) = v(r(t)) dt

Ist die Kurve eben mit der Darstellung y = y(x) mit a < x < b, dann folgt:

integral b V~ ---'2---- T(y) = --1+-y-(x)dx != Minimum auf D a v(x,y(x))

[next] [prev] [prev-tail] [front] [up]