1.4 Das Problem der Brachystochrone

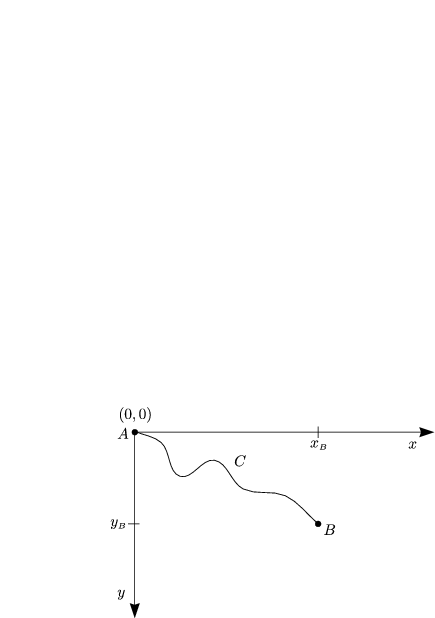
Durch 2 Punkte A und B in einer senkrecht gedachten Ebene ist eine Kurve C so zu legen, daß ein Massenpunkt, der sich längs C nur unter dem Einfluß der Schwerkraft bewegt, in kürzester Zeit von A nach B gelangt.

Nach dem Energieerhaltungssatz gilt nun:

1mv2 - mgy = 0 2

Damit erhalten wir durch Auflösen v:

V~ --- v = 2gy

Gesucht ist nun y = y(x) mit y(0) = 0, y(x_B) = y_B, daß folgender Ausdruck minimal wird für y ¹[0,x_B]:

integral xB V~ ---'--2- T(y) = V~ -1 1+-y-(x)--dx 2g y(x) 0

Das Integral ₀^x_B muß damit existieren für y(x) > 0. Wir vertauschen einfach die Bezeichnungen der Achsen oben. T(y) lautet jetzt:

|--------------------------| | ~x integral B V~ -------- | |T(y) = V~ 1- 1-+y'(x)dx | | 2g x | ------------0--------------

Dies stellt nun kein Problem dar, da das Integral ₀^x_B existiert.

[next] [prev] [prev-tail] [front] [up]