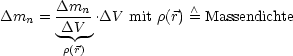

![N ( ) ( ) [ ( ) ]
E = sum 1m V2 = 1 s um m V 2+ 1.2.V × _O_ s um m .r + 1 sum m _O_2r2- _O_ .r 2
kin n=1 2 n n 2 n n 0 2 0 n n n 2 n n n n
--- --- --- --- ----------- -----------
M (Gesamtmasse) M.rs Rotationsnergie](th590x.gif)
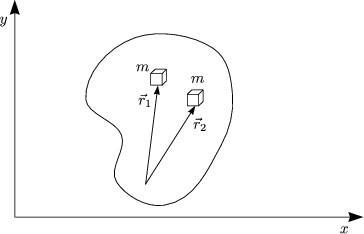
Wie wählen den Ursprung des körperfesten Koordinatensystems im Schwerpunkt, so daß die Kopplung zwischen Translation und Rotation verschwindet!
![N
Erot = 1 sum mn [(_O_2 + _O_2 +_O_2 )(x2 + y2+ z2)- (_O_xxn +_O_yyn + _O_zzn)2]=
2n=1 x y z n n n
1 sum
= 2 Ikl_O_k_O_l
k=k1l,2,3
<==>x,y,z](th591x.gif) | (5.1) |
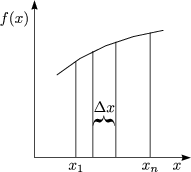
![]() x ist der Abstand von der x-Achse.
x ist der Abstand von der x-Achse.
![]() ist der Spaltenvektor der Rotationsgeschwindigkeit. Bei I handelt es sich um eine
3 × 3-Matrix (Ixx, Ixy, ...), nämlich der sogenannten Trägheits(-matrix).
ist der Spaltenvektor der Rotationsgeschwindigkeit. Bei I handelt es sich um eine
3 × 3-Matrix (Ixx, Ixy, ...), nämlich der sogenannten Trägheits(-matrix). ![]() hängt
nicht____ von der Wahl des körperfesten Koordinatensystems ab.
hängt
nicht____ von der Wahl des körperfesten Koordinatensystems ab.
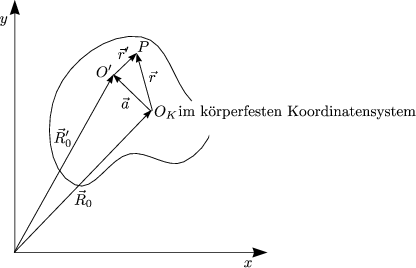
Für alle Punkte P gilt ![]() =
= ![]() '
.
'
.
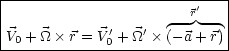
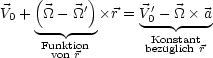
Daraus ergibt sich dann ![]() =
= ![]() ' und
' und ![]() 0 =
0 = ![]() 0'-
0'-![]() ×
×![]() .
.
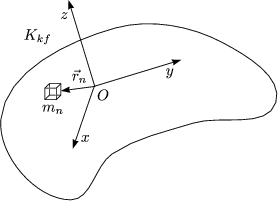
Die Energie ergibt sich als Summe aus Translationsenergie des Schwerpunkts und Rotationsenergie um Schwerpunkt. Für den Drehimpuls gilt:
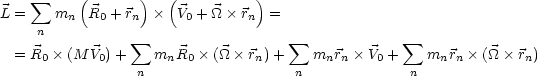 | (5.2) |
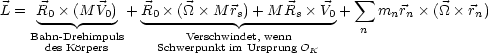
Im allgemeinen ist ![]() nicht parallel zu
nicht parallel zu ![]() , selbst wenn
, selbst wenn ![]() 0 =
0 = ![]() . Ikl besteht aus 9
Größen und ist außerdem symmetrisch (Ikl = Ilk). Es gibt somit nur 6 unabhängige
Größen! Da Ikl symmetrisch ist, existiert außerdem ein Koordinatensystem, in dem I
diagonal ist.
. Ikl besteht aus 9
Größen und ist außerdem symmetrisch (Ikl = Ilk). Es gibt somit nur 6 unabhängige
Größen! Da Ikl symmetrisch ist, existiert außerdem ein Koordinatensystem, in dem I
diagonal ist.

Wie findet man das Hauptachsensystem?
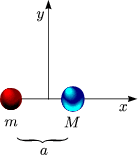
Es handelt sich um punktförmige Massen.
Bei mathematischen Pendel ist die kinetische Energie gleich:
Für das Zweikörperproblem haben wir:
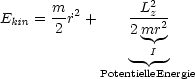
Wie berechnet man ![]() nmn .
nmn .![]() ?
?
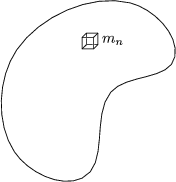
Man bildet den Grenzwert für N (Anteil der Moleküle) ![]()
![]() und erhält somit ein
Volumenintegral.
und erhält somit ein
Volumenintegral.